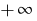Definition: eine Abhängigkeit einer Variablen 
von einer Variablen 
heißt Funktion, wenn jedem Wert der einzige Wert entspricht .
Die Funktion wird durch oder einem Buchstaben 
, (oder 
), oder Gleichheit 
.
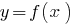Definition: eine Numerische Funktion mit dem Bereich der Bestimmung der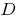 
Abhängigkeit genannt, bei der jede Zahl aus der Menge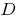 wird in übereinstimmung Singular , was natürlich wirkt .
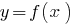Termine: —unabhängige Variable oder argument, unabhängige Variable oder Funktion,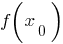 
—den Wert der Funktion an der Stelle 
Der Bereich der Bestimmung der Funktion
Definition: das Gebiet von Funktionen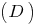 
— die Menge jener Werte, die das argument annehmen kann.
Beispiel für die Feststellung der Definitionsbereich der Funktion
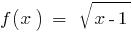
Bereich Definition (EN):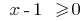 
, D. H.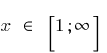 
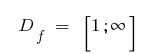
Viele Werte der Funktion
Definition: die Menge der Werte von Funktionen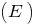 
— die Menge der Werte, die Sie annehmen kann, die Funktion bei allen Werten Argumente aus dem Bereich der Definitionen (es werden alle Werte >m>a, wenn die Gleichung 
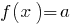hat die Entkopplung).
Beispiel für die Feststellung der Menge der Funktionswerte
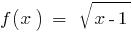
Viele Bedeutungen: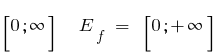 
, da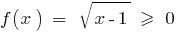 
für alle 
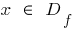und nimmt alle Werte von 0 bis 