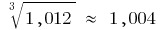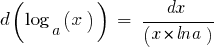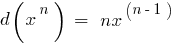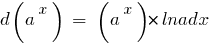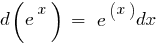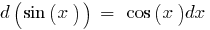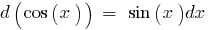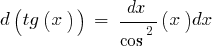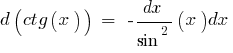Der Begriff des Differenzials
Definition: Differential der Funktion 
an der Stelle 
bezeichnet das Werk Ableitung 
in diesem Punkt, d.h. 
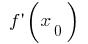auf die Zunahme des Arguments 
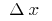(durch 
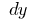oder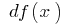 
— lesbar "DAE Y.")
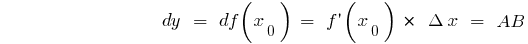
Für jeden Punkt 
: 
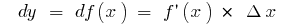wenn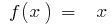 
, haben 
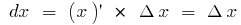, dann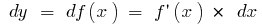 
Tabelle der elementaren Differentiale der Funktionen:
Ein Beispiel finden Differential in der Mathematik:
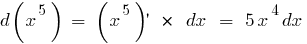
Differenzial strukturierten Funktionen
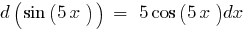
Die wichtigste Eigenschaft des Differenzials
Differenzial-Funktion-Home-lineare (proportionale 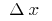) Teil des Zuwachses der Funktion
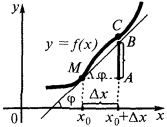
Der Verbleib des Differenzials. Geometrische Bedeutung des Differentials.
Die Regeln des seins Differentialsperre bleiben die gleichen wie für die Suche nach Derivat, muss man nur multiplizieren Ableitung auf DX.
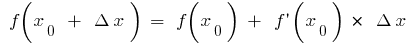
Wenn in der Formel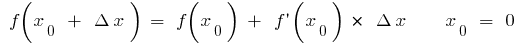 
(wenn vorhanden 
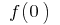und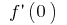 
), das für kleine 
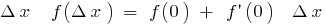. Wir bezeichnen 
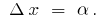Dann für kleine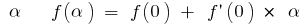 
Zum Beispiel:
a) für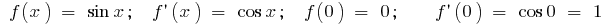 
, D. H. 
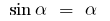(für die kleinen 
) ;
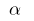B)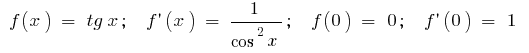 
, D. H. 
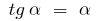(für die kleinen )
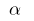Beispiel zur Berechnung der Differentiale Für die näherungsweise Berechnung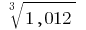 
nehmen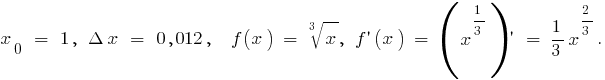 
Dann ist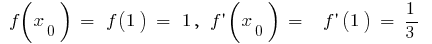 
die Formel 
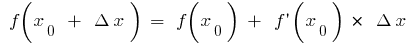gibt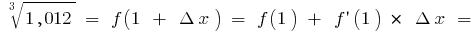 
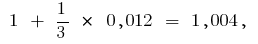das heißt 