Definition: Показниково-exponentiale Gleichung  — Gleichung, die Art des Ausdrucks
— Gleichung, die Art des Ausdrucks 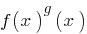 , das heißt die Gleichungen der Art
, das heißt die Gleichungen der Art 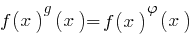
Grundsätzliches zur Lösung показниково-exponentielle Gleichungen und Ungleichungen
 Für den Fall f(x)>0
Für den Fall f(x)>0
Beispiel 1
Lösung:
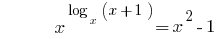
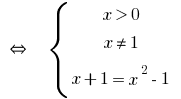
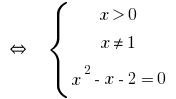
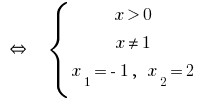
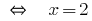
Antwort: 
Beispiel 2
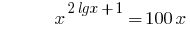
Lösung:
Auf DHS  beide Teile der Gleichung sind positiv, also nach логарифмирования zur Basis 10, so erhalten wir die Gleichung, was gleichbedeutend ist mit dieser
beide Teile der Gleichung sind positiv, also nach логарифмирования zur Basis 10, so erhalten wir die Gleichung, was gleichbedeutend ist mit dieser 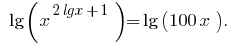
Von hier 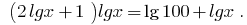
Ersatz 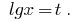
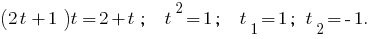
Dann 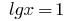 oder
oder 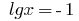 , d.h.
, d.h. 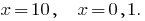 (beide Wurzel führen zu DHS)
(beide Wurzel führen zu DHS)
Antwort: 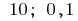
 Für den Fall f(x) — jeder beliebige Ausdruck
Für den Fall f(x) — jeder beliebige Ausdruck
Beispiel 3
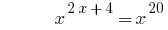
Lösung:
Wenn man die Basis  der Zahl, dann
der Zahl, dann
1) wenn 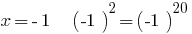 die richtige Gleichheit;
die richtige Gleichheit;
2) bei 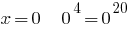 richtig;
richtig;
3) wenn 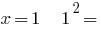 richtig;
richtig;
4) wenn 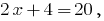 dann eine
dann eine 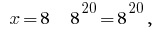 richtige Gleichheit.
richtige Gleichheit.
Antwort: 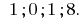
Hinweis: Wenn als Grundlage  der Variablen, wird die Funktion
der Variablen, wird die Funktion 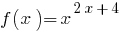 gilt nur die bei
gilt nur die bei 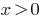 . Aus dieser Sicht ist diese Gleichung haben nur zwei Wurzeln:
. Aus dieser Sicht ist diese Gleichung haben nur zwei Wurzeln: 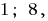

 Für den Fall f(x)>0
Für den Fall f(x)>0