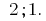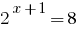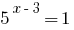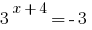Lagersitz-Fakten
Jede zunehmenden (abnehmenden) Funktion auf dem Intervall jeder gewinnt Ihre Bedeutung nur in einem Punkt von dieser Lücke.
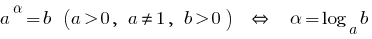
Bei der 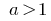 exponential-Funktion
exponential-Funktion  erhöht.
erhöht.
Bei  kommt.
kommt.
Bei der 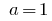 exponential-Funktion
exponential-Funktion  geworden.
geworden.
Nach der Entscheidung exponentielle Gleichungen zu kennen die Eigenschaften von Wurzeln und Stufen.
Auch die Beseitigung einfacher bezeichnenden Gleichungen
Lösung:
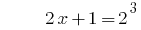
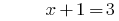
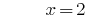
Antwort: 
Lösung:
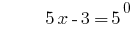
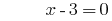
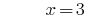
Antwort: 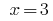
Lösung:
Wurzeln nicht (so 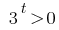 )
)
Antwort:die Wurzeln nicht
Lösung:
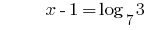
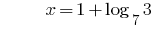
Antwort: 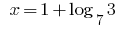
Auch die Entscheidung repräsentativer quadrieren von Gleichungen auf das einfachste
______________________________________________________________________
Wenn im linken und rechten Teil exponential-Gleichungen sind nur Werke, Brüche, Wurzeln AO Grad, ist es ratsam, mit grundlegenden Formeln versuchen, brennen beide Teile Gleichungen wie der Grad mit einer Basis.
______________________________________________________________________
Beispiel 1:
Розвяжіть Gleichungen 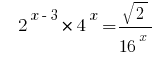 .
.
Lösung:
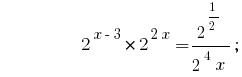
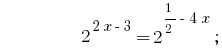
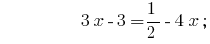
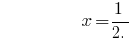
Antwort: 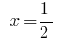 .
.
______________________________________________________________________
Wenn in einem Teil der exponential-Gleichungen steht eine Zahl, in der anderen alle Mitglieder die ein Ausdruck der Art 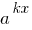 (Indikatoren Abschlüsse unterscheiden sich nur Mitglieder frei), wird bequem in diesem Teil der Gleichung Luftschutzkeller Grad das kleinste
(Indikatoren Abschlüsse unterscheiden sich nur Mitglieder frei), wird bequem in diesem Teil der Gleichung Luftschutzkeller Grad das kleinste  .
.
______________________________________________________________________
Beispiel 2:
Розвяжіть Gleichungen 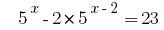 .
.
Lösung:
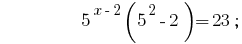
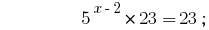
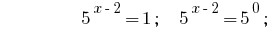
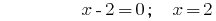
Antwort: 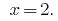 .
.
Beispiele für die Lösung von komplexeren bezeichnenden Gleichungen
______________________________________________________________________
Befreien Sie sich von den numerischen Faktoren in Bezug auf Abschlüsse (von rechts nach Links mit grundlegenden Eigenschaften von Abschlüssen).
Wenn möglich, reduzieren wir alle Grad zu einem Boden und führen den Ersatz der Variablen.
______________________________________________________________________
Beispiel 3:
Розвяжіть Gleichungen 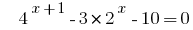 .
.
Lösung:
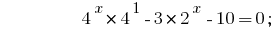
Wenn man bedenkt, dass 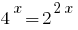 , reduzieren Grad zu einer Basis 2:
, reduzieren Grad zu einer Basis 2: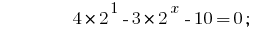
Ersatz 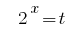 gibt die Gleichung:
gibt die Gleichung:
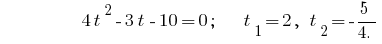
Reverse Ersatz gibt eine Gleichung 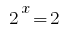 , Woher
, Woher  oder
oder 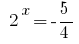 - Wurzeln nicht.
- Wurzeln nicht.
Antwort: 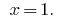
______________________________________________________________________
Wenn nicht Grad reduziert werden auf eine Basis, dann versuchen, möglichst alle Freiheitsgrade auf zwei Grundlagen, um homogene Gleichung.
______________________________________________________________________
Beispiel 4:
Розвяжіть Gleichungen 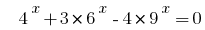 .
.
Lösung:
Lasst uns hier alle Grad auf zwei Grundlagen 2 und 3:
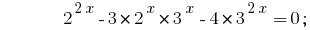
Haben homogene Gleichung. Für seine Entscheidung dividieren beide Seiten durch 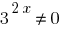 ;
;
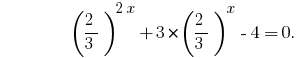
Ersatz 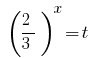 gibt die Gleichung:
gibt die Gleichung:
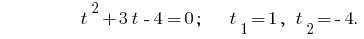
Reverse Ersatz gibt eine Gleichung 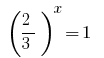 , Woher
, Woher 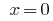 oder
oder 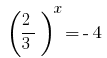 - Wurzeln nicht.
- Wurzeln nicht.
Antwort: 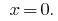
______________________________________________________________________
In anderen Fällen übertragen wir alle Mitglieder der Gleichungen in einen Teil zerlegen und versuchen das resultierende Ausdruck auf Multiplikatoren oder wenden spezielle Techniken der Bewältigung, in denen nutzen die Eigenschaften der entsprechenden Funktionen.
______________________________________________________________________
Beispiel 5:
Розвяжіть Gleichungen 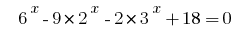 .
.
Lösung:
Wenn paarweise gruppieren Mitglieder im linken Teil der Gleichung und in jedem paar Luftschutzkeller gemeinsame Vielfache (KGV), erhalten wir :
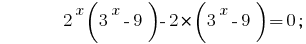
Nehmen Sie für gemeinsame Vielfache (KGV) Klammern 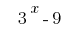 :
:
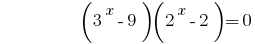
Dann 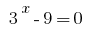 oder
oder 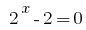 .
.
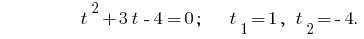
Wir erhalten die beiden Gleichungen 1)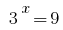 , Woher
, Woher  oder 2)
oder 2)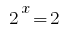 , wo
, wo  .
.
Antwort: