Definition: die Geometrische Progression  — Zahlenfolge, der erste term von null Verschieden, und jedes Mitglied, beginnend mit dem zweiten, gleich dem vorhergehenden Glied, multipliziert mit der auf die gleiche Zahl, die nicht gleich null sind.
— Zahlenfolge, der erste term von null Verschieden, und jedes Mitglied, beginnend mit dem zweiten, gleich dem vorhergehenden Glied, multipliziert mit der auf die gleiche Zahl, die nicht gleich null sind.
Definition: Nenner exponentiell  — Konstante für die Anzahl der Sequenzen
— Konstante für die Anzahl der Sequenzen 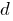 , die multiplizieren auf jedes Mitglied.
, die multiplizieren auf jedes Mitglied.
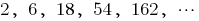 — geometrische Progression,
— geometrische Progression, 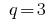
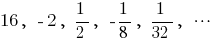 — geometrische Progression,
— geometrische Progression, 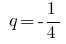
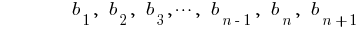 — geometrische Progression
— geometrische Progression
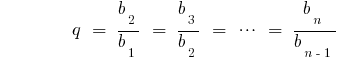 — Nenner exponentiell
— Nenner exponentiell
Charakteristischen Eigenschaften der geometrischen Progression
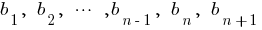
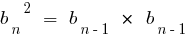
Eigenschaft: Quadrat jedes Mitglied exponentiell (ab dem zweiten Mitglied) gleich dem Produkt der vorhergehenden und der nachfolgenden Mitglieder und Umgekehrt, wenn Sie die angegebene властивіть, dann wird die Sequenz geometrischer Progression.
Formel n-TEN Mitglieds exponentiell
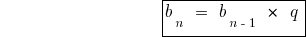
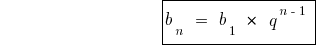
Formel Summe der n ersten Glieder einer geometrischen Progression
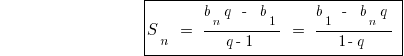
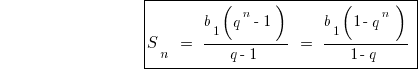
Plan der Lösung von Aufgaben auf die geometrische Progression
- Alles, worum es in der Rede-Aufgaben (Mitglieder der Fortschritt, deren Summe, etc), die wir durch das erste Bauteil und die Differenz der Progression.
- Bilden eine Gleichung (oder ein System von Gleichungen) durch die Bedingung der Aufgabe. In dem Fall, wenn in der Aufgabe gibt es einen übergang von exponentiell zu Linear und Umgekehrt, für die Erstellung von Gleichungen verwenden in der Regel die charakteristischen Eigenschaften der Progressionen.
Unendlich abnehmenden geometrischen Progression
Definition: Unendlich abnehmenden geometrischen Progression ist eine unendliche geometrische Progression, dem Nenner modulo kleiner als eins
ist eine unendliche geometrische Progression, dem Nenner modulo kleiner als eins 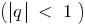 .
.
Beispiel
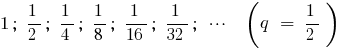
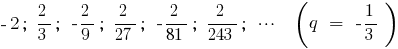
Definition: die Summe der unendlich abnehmenden geometrischen Progression — Grenze anstreben, die Summe  Ihrer ersten Mitglieder, bei einer unendlichen Wachstum
Ihrer ersten Mitglieder, bei einer unendlichen Wachstum  .
.
.
Die Formel zur Berechnung der Summe der unendlich abnehmenden geometrischen Progression

Beispiel für die Feststellung der Summe der unendlich abnehmenden geometrischen Progression
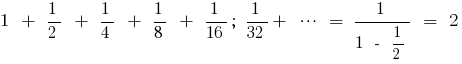
Umwandlung periodischer Dezimalbrüche in gewöhnliche
Beispiel
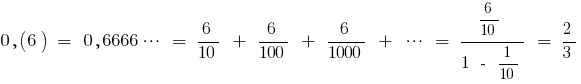 (als Summe der unendlich abnehmenden geometrischen Progression mit dem ersten Mitglied
(als Summe der unendlich abnehmenden geometrischen Progression mit dem ersten Mitglied 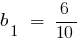 und Nenner
und Nenner 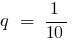 )
)
