Definition:eine Funktion der Art 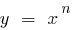 , wo n — eine beliebige reelle Zahl, genannt der exponentiellen Funktion
, wo n — eine beliebige reelle Zahl, genannt der exponentiellen Funktion
Eigenschaften der exponentiellen Funktion (bei 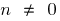 )
)
a) n — Natürliche  b) n — eine ganze відємне
b) n — eine ganze відємне  c) n — nicht die ganze
c) n — nicht die ganze
a)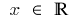
b)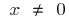
c) bei 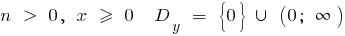
 bei
bei 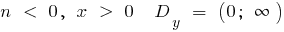
a) bei n Doppel 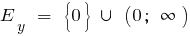
 wenn n ungerade
wenn n ungerade 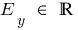
b) bei n Doppel 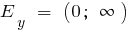
 wenn n ungerade
wenn n ungerade 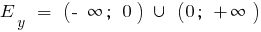
c) bei 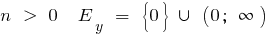
 bei
bei 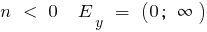
a),b) bei n Doppel — Dampfbad
 bei n ungerade — ungerade
bei n ungerade — ungerade
c) weder gerade noch ungerade
nicht periodische
a) 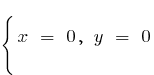
b) Nein
c) bei 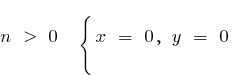
 wenn
wenn  — Nein
— Nein
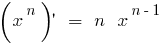
a) bei n Doppel 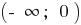 — abnehm,
— abnehm,  — erhöht
— erhöht
 bei n ungerade — wächst
bei n ungerade — wächst
b) bei n Doppel 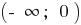 — zunimmt,
— zunimmt,  — abnimmt
— abnimmt
 bei n ungerade
bei n ungerade 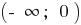 — kommt
— kommt  — kommt
— kommt
c) bei 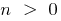 — wächst
— wächst
 bei
bei  — kommt
— kommt
a) bei n Doppel 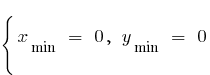
 bei n sonderbaren — Nein
bei n sonderbaren — Nein
b) Nein
c) bei 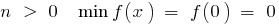
 wenn
wenn 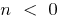 — Nein
— Nein
a) Nein
b) 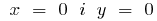
c) wenn 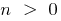 Nein
Nein
 bei
bei 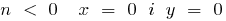
a) bei n Doppel  — Wölbung nach unten
— Wölbung nach unten
 wenn n ungerade,
wenn n ungerade, 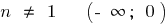 —
— 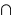 ;
;  —
—  ; 0 — Wendepunkt
; 0 — Wendepunkt
b) bei n Doppel — 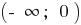 —
—  ;
;  —
— 
 bei n ungerade —
bei n ungerade — 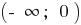 —
— 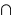 ;
;  —
— 
c) bei 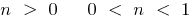 —
— 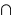 ;
; 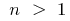 —
— 
 bei
bei 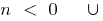
Wenn 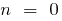 , dann
, dann 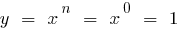 (wenn
(wenn 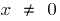 )
)
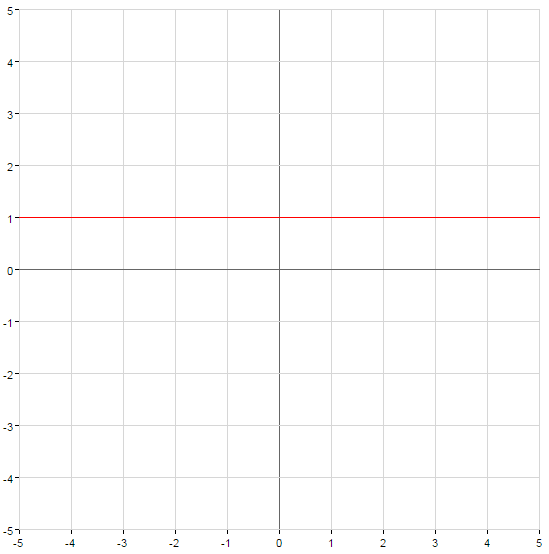
- Das Gebiet

- Mehrfacher Wert

- Parität, ungerade
- Periodizität
- Der Schnittpunkt der Achsen des
- Derivat
- Aufsteigend und absteigend
- Extrema
- Asymptoten
- Ausbuchtung und den Eckpunkt
- Besonderen Anlass
Grafik exponentielle Funktionen

- n — eine gerade Natürliche Zahl
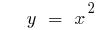
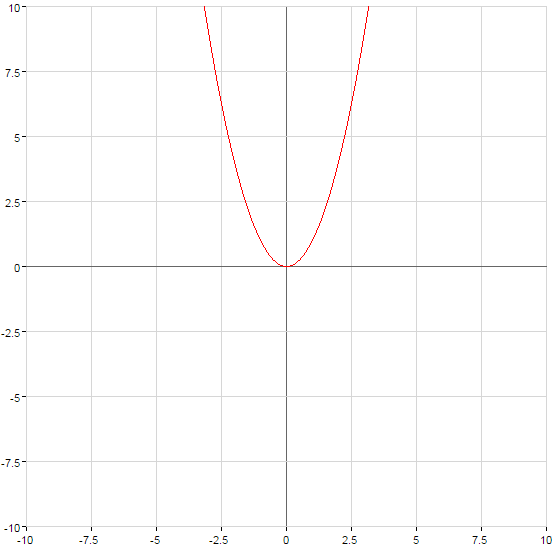
- n — ungerade Natürliche Zahl
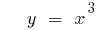
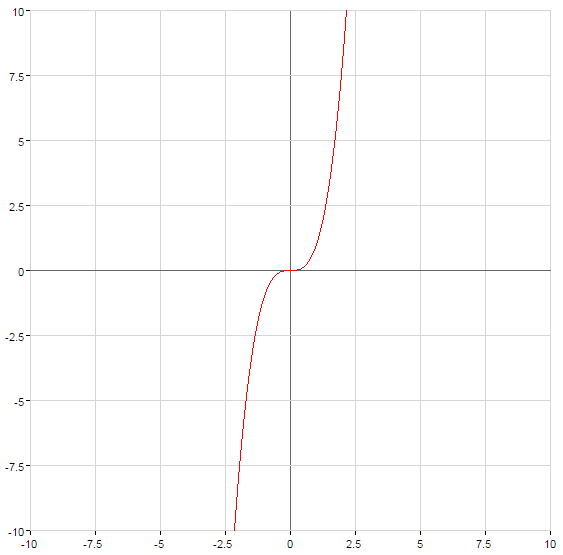
- n — ungerade Zahl відємне
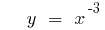
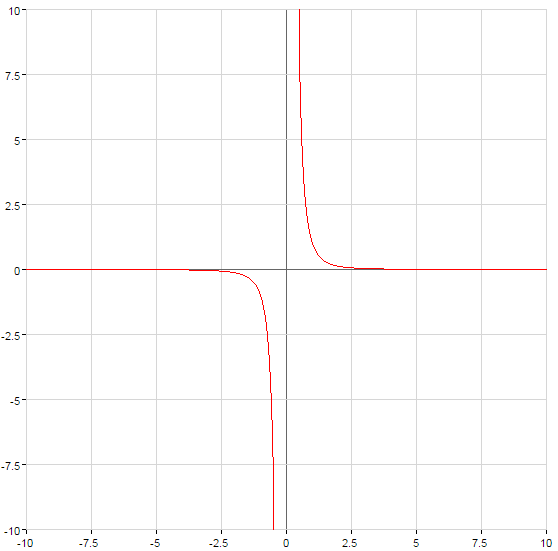
- n — gerade Zahl відємне
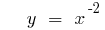
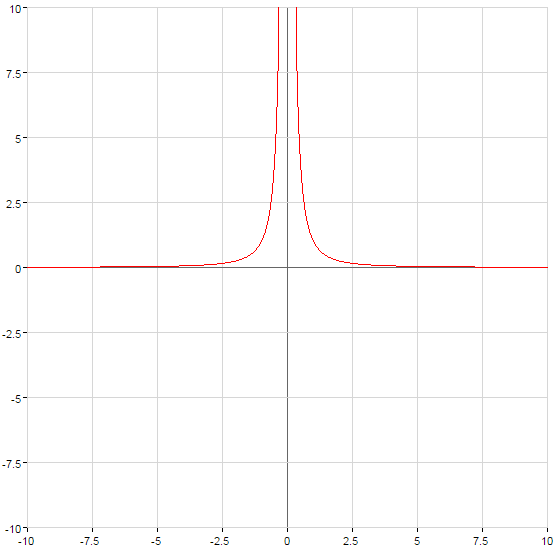
- n — eine positive ganze Zahl nicht
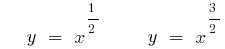 (grün)
(grün)
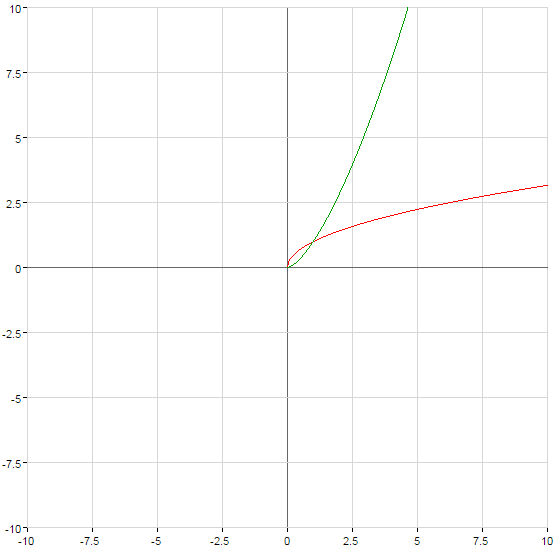
- n — nicht eine ganze Zahl відємне
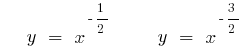 (grün)
(grün)
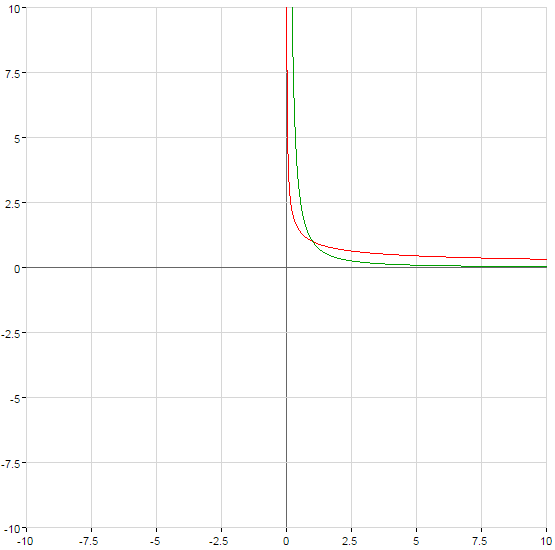

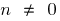 )
)
