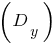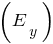Definition: the Function of the form 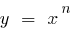 where n is any real number, is called power function
where n is any real number, is called power function
Properties of the power function (in 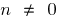 )
)
a) n — natural  b) n is an integer WMA
b) n is an integer WMA  c) n is not a whole
c) n is not a whole
- Scope
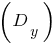
- Multiple value
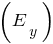
- Parity, odd parity
- The frequency
- The intersection with the coordinate axes
- Derivative
- The increase and decrease of
- Extrema
- Asymptotes
- Convexity and points of inflection
- A special case
a)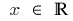
b)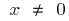
c) when 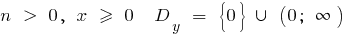
 when
when 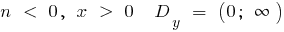
a) when n doubles 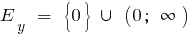
 when n is odd
when n is odd 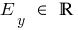
b) when n doubles 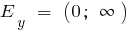
 when n is odd
when n is odd 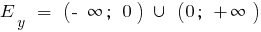
c) when 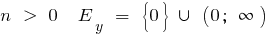
 when
when 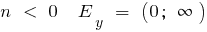
a),b) when n doubles — doubles
 when n is odd — odd
when n is odd — odd
c) neither even nor odd
not periodic
a) 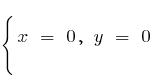
b) no
c) when 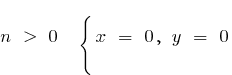
 when
when  — no
— no
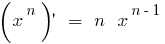
a) when n doubles 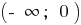 — decreases,
— decreases, 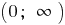 increases
increases
 when n odd — is growing
when n odd — is growing
b) when n doubles 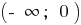 — increases
— increases 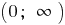 — decreases
— decreases
 when n odd
when n odd 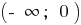 — comes
— comes 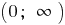 — comes
— comes
c) when 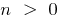 — growing
— growing
 when it
when it  comes
comes
a) when n doubles 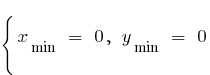
 when n is odd — no
when n is odd — no
b) no
c) when 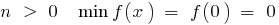
 when
when 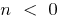 — no
— no
a) no
b) 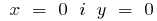
c) while 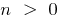 — not
— not
 when
when 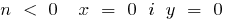
a) when n doubles 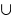 — bulge down
— bulge down
 when n is odd,
when n is odd, 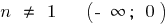 —
— 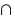 ;
; 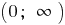 —
— 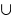 ; 0 — inflection point
; 0 — inflection point
b) when n doubles — 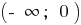 —
— 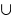 ;
; 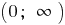 —
— 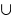
 when n is odd —
when n is odd — 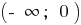 —
— 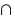 ;
; 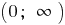 —
— 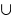
c) when 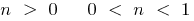 —
— 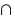 ;
; 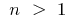 —
— 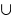
 when
when 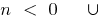
If 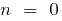 ,
, 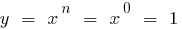 (when
(when 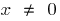 )
)
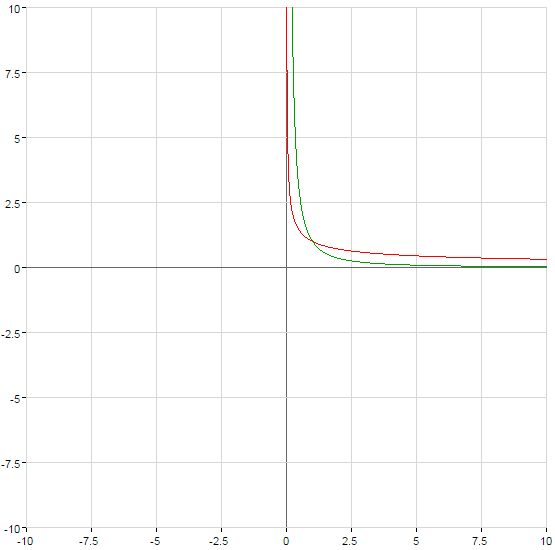
Graphs of power functions

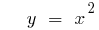
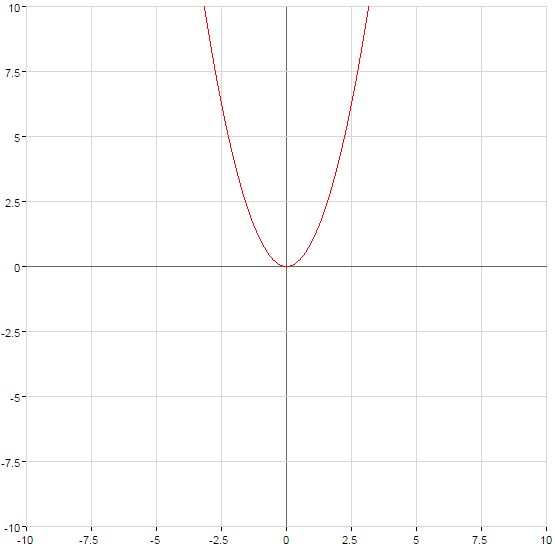
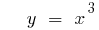
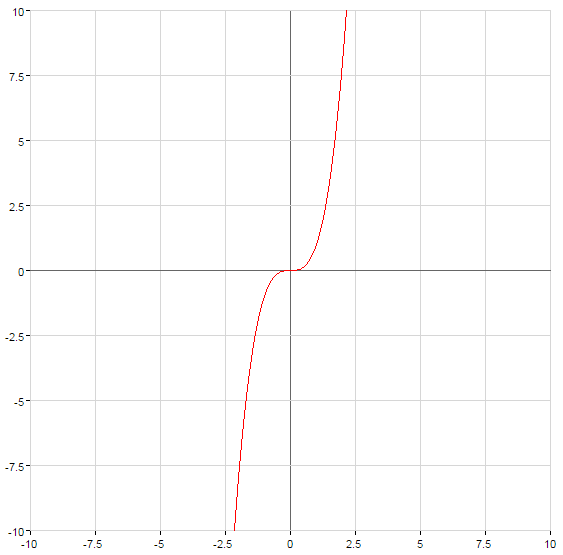
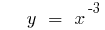
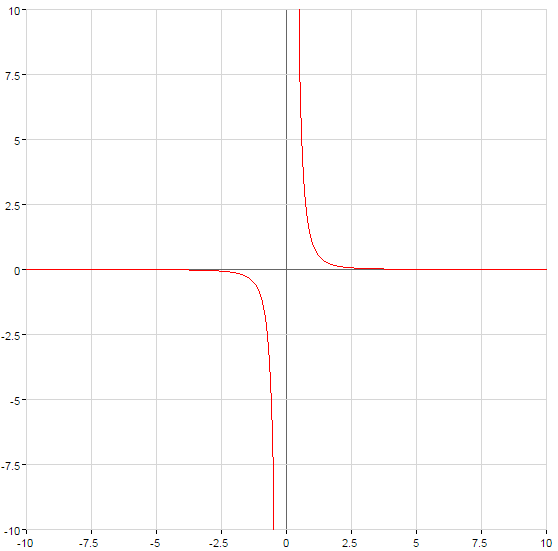
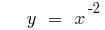
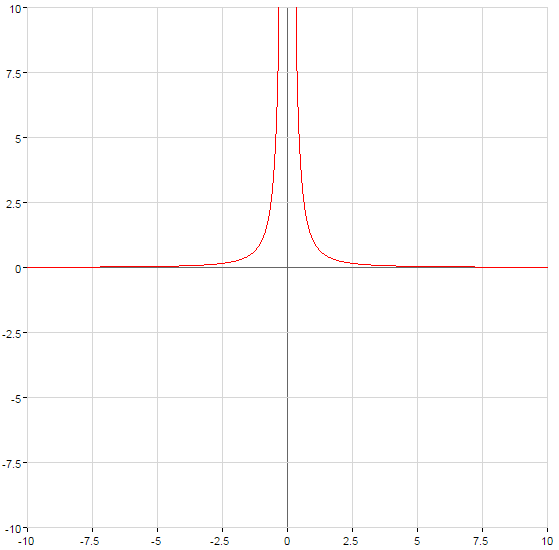
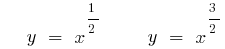 (green)
(green)
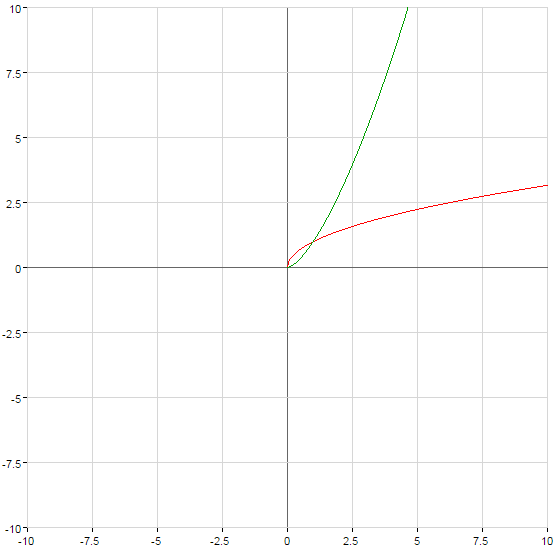
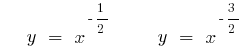 (green)
(green)

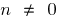 )
)