Definition:If a function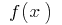 
defined on an interval 
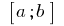and 
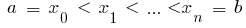then a definite integral of a function 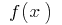on an interval 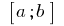is a number equal to limit of integral sum 
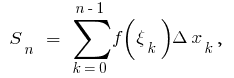where 
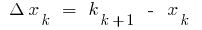f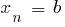 
that is
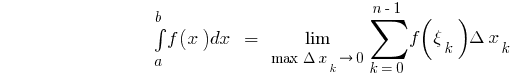
where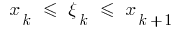 
i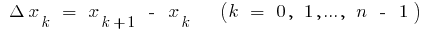 
The construction of integral sums for the example of determining the area of the curvilinear trapezoid
Let on the segment 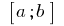is set to an integral and continuous function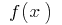
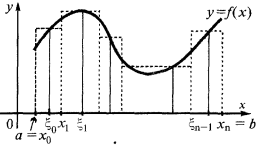
To determine the area of the curvilinear trapezoid (bounded curve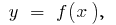 
axis 
and straight, 
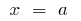and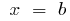 
), divide the cut 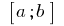points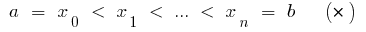 
on the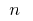 
parts selected on each of the obtained partial segments 
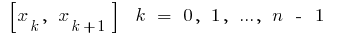of an arbitrary point of the 
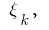calculated values
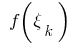of the function 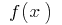at these points and form the sum 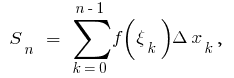where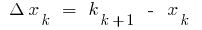
This amount is equal to the sum of the areas of the shaded rectangles is called the integral sum.
If now the number of dividing points increases indefinitely, and the length max (highest) partial cut partitioning tends to zero, and the value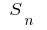 
tends to a certain limit 
does not depend on the method of division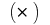 
and the choice of points 
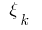on partial segments, then the value 
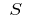is called the area of the curvilinear trapezoid, i.e.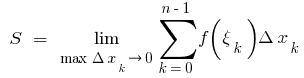 
The Formula Newton - Leibniz
If the function is 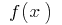defined and continuous on the interval 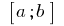and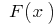 
is its integral (i.e. 
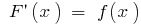), then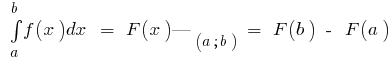 
Example. As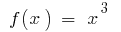 
one of the primitive 
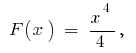then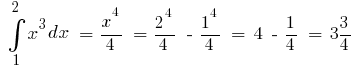 
The basic properties of the definite integral
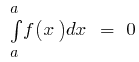
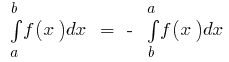
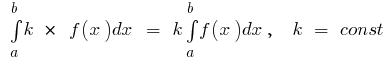
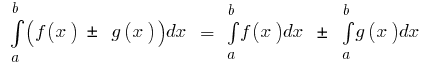
- If
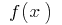integrated on 
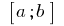and 
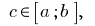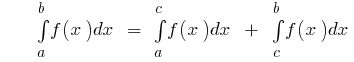
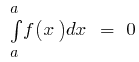
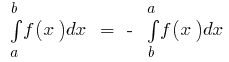
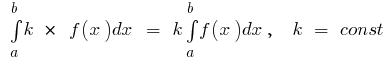
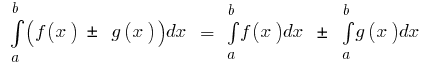
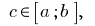then
then