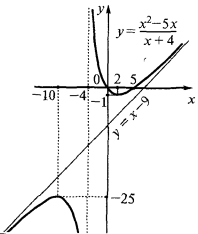
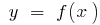Example. 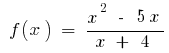
- Scope
- Parity, odd parity, periodicity
- The intersection with the coordinate axes
- The derivative and critical points
- Intervals of increase, decrease, and extreme points (and the value of the function at these points)
- The behavior of the functions at the ends of the scope and the asymptotes of the graph of a function (vertical, horizontal and inclined)
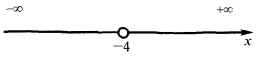
When you
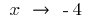 left
left 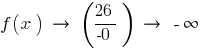
In
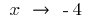 the case
the case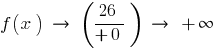
Therefore,
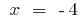 — vertical asymptote
— vertical asymptoteSince
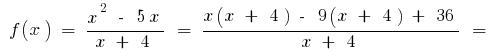
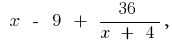 when
when 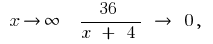 then
then 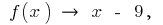 ie
ie 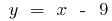 is the oblique asymptote
is the oblique asymptote - The second derivative and the study of the function of the bulge and gnutt
- If you want to find control points specifying the behavior of the graph
- On the basis of the study building sketch the graph of a function
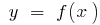
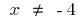
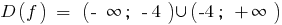
The function is neither even nor odd and periodic
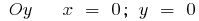
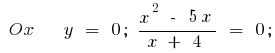
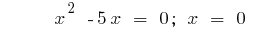 or
or 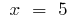
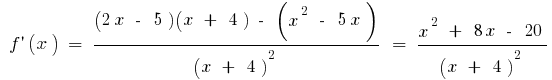
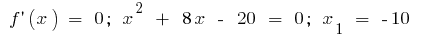 or
or 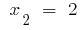
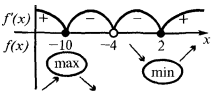
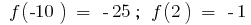
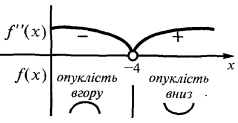
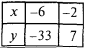
Find the inflection points (if they exist) and values 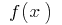 in the points of inflection
in the points of inflection
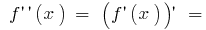
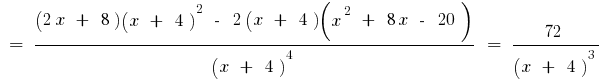
So 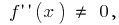 the sign of the second derivative can change only at the point
the sign of the second derivative can change only at the point 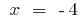


 left
left 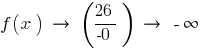
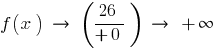
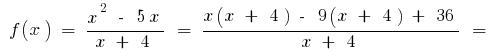
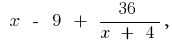 when
when 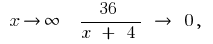 then
then 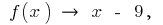 ie
ie 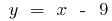 is the oblique asymptote
is the oblique asymptote