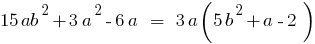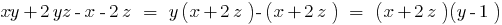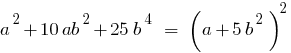Algebraic expressions a single term and a polynomial

A single term

Definition: a single term is called a finite product of numbers, letters, and their natural degree, and the numbers, letters and their degree.

A single term is zero — the number 0.

Definition: the Degree of a single term is the sum of the letters that is included in a single term. If a single term is a number that is not zero, its degree is considered to be zero.

A single term written in standard form if the first multiplier is a number, called the coefficient of a single term.

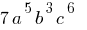— a single term in standard form

Such a single term, if they are equal or differ only in their coefficients.

Operations on monomials

1. Addition and subtraction



2. Multiplication



3. Exponentiation



4. Division

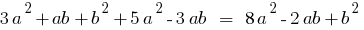
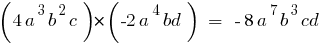
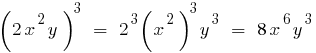
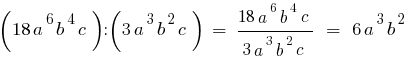
The polynomial

Definition: Polynomial — the sum of a finite number of a single term (each of which is a member of the polynomial).

A single term consisting of one member are also considered polynomials.

The number 0 is called the zero polynomial

Examples of polynomials

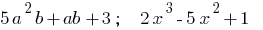— polynomials

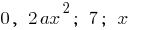— polynomials consisting of one member

Definition: the Degree of a nonzero polynomial is the greatest degree of the degrees of its members (a single term).

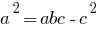— the polynomial of the third order (because the highest degree 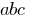is the third)

Polynomial zero (0) degree has not.

Actions on polynomials

1. Add



2. Subtraction



3. Multiplication

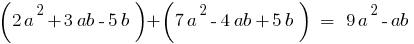
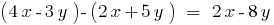
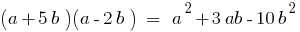
Identically equal polynomials

Definition: Two polynomials equal if they acquire runic values for all values of the letters.

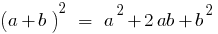
The decomposition of a polynomial into factors

1. The imposition of a common multiplier of the bracket



2. The grouping method



3. The use of formulas of reduced multiplication