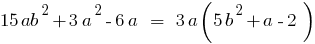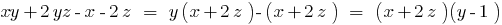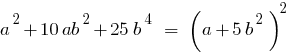Алгебраические выражения, одночлен и многочлен

Одночлен

Определение: Одночленом называется конечный произведение чисел, букв и их натуральных степеней, а также сами числа, буквы и их степени.

Нулевой одночлен — число 0.

Определение: Степень одночлена — это сумма показателей букв, что входит в одночлен. Если одночленом является число, что не равно нулю, то его степень считается равным нулю.

Одночлен записан в стандартном виде, если первый множитель есть число, называется коэффициентом одночлена.

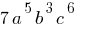— одночлен в стандартном виде

Подобные одночлен, если они равны между собой или различаются только своими коэффициентами.

Действия над одночленами

1. Сложение и вычитание



2. Умножение



3. Возведение в степень



4. Деление

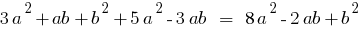
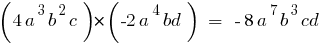
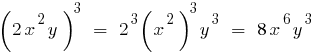
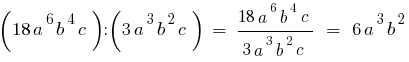
Многочлен

Определение: Многочлен — сумма конечного числа одночлен (каждый из которых называется членом многочлена).

Одночлен, состоящие из одного члена также считаются многочленами.

Число 0 называется нулевым многочленом

Примеры многочленов

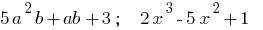— многочлены

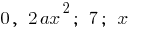— многочлены, состоящие из одного члена

Определение: Степень ненулевого многочлена —наибольший степень из степеней его членов (одночлен).

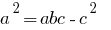— многочлен третьей степени (поскольку наибольший степень — третий)

Нулевой многочлен (0) степени не имеет.

Действия над многочленами

1. Добавление



2. Вычитание



3. Умножение

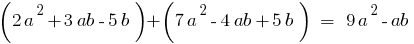
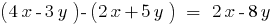
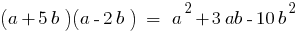
Тождественно равные многочлены

Определение: Два многочлена тождественно равны — если они приобретают рвних значений при любых значениях букв.

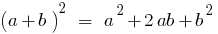
Разложение многочлена на множители

1. Вынесение общего множителя за скобку



2. Метод группировки



3. Использование формул сокращенного умножения