Определение: Показниково-степенное уравнение  — уравнение, содержащее выражения типа
— уравнение, содержащее выражения типа 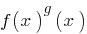 , то есть уравнения вида
, то есть уравнения вида 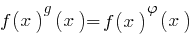
Основные способы решению показниково-степенных уравнений и неравенств
 Для случая f(x)>0
Для случая f(x)>0
Пример 1
Решения:
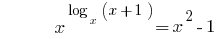
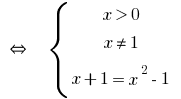
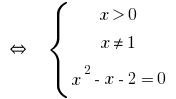
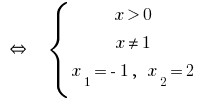
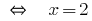
Ответ: 
Пример 2
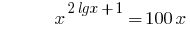
Решения:
На ОДЗ  обе части уравнения положительны, поэтому после логарифмирования по основанию 10, получаем уравнение, равносильное данному
обе части уравнения положительны, поэтому после логарифмирования по основанию 10, получаем уравнение, равносильное данному 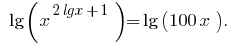
Отсюда 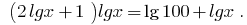
Замена 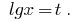
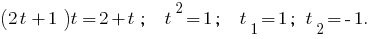
Тогда 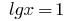 или
или 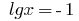 , т. е.
, т. е. 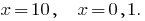 (оба корня водят к ОДЗ)
(оба корня водят к ОДЗ)
Ответ: 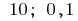
 Для случая f(x) — произвольное выражение
Для случая f(x) — произвольное выражение
Пример 3
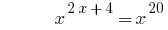
Решения:
Если считать основу  числом, то
числом, то
1) при 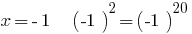 правильная равенство;
правильная равенство;
2) при 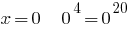 правильно;
правильно;
3) при 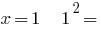 правильно;
правильно;
4) при 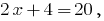 то есть
то есть 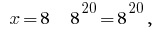 верное равенство.
верное равенство.
Ответ: 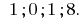
Замечание: Если считать основу  переменной, то функция
переменной, то функция 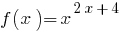 считается возникшим лишь при
считается возникшим лишь при 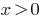 . С этой точки зрения данное уравнение будет иметь только два корня:
. С этой точки зрения данное уравнение будет иметь только два корня: 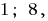

 Для случая f(x)>0
Для случая f(x)>0