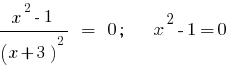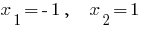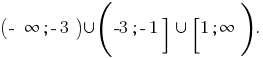Решению неравенств с помощью равносильных преобразований
- Преобразования, гарантирующие сохранение правильной равенства
- Проверка корней подстановкой в исходное неравенство
Решению уравнений с помощью метода интервалов
- Найти ОДЗ.
- Найти нули функции:

- Отметить нули на ОДЗ и найти знак функции f(x) в каждом промежутке, на которые разбивается ОДЗ.
- Записать ответ, учитывая знак заданного неравенства.
Решению неравенств. Метод интервалов.
- Найти ОДЗ.
- Найти нули функции:

- Отметить нули на ОДЗ и найти знак функции f(x) в каждом промежутке, на которые разбивается ОДЗ.
- Записать ответ, учитывая знак заданного неравенства.
Пример 1.
Розвяжіть неравенство: 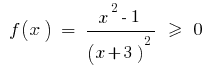
Розвязання. Пусть 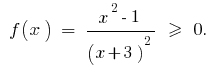
- ОДЗ:
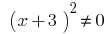 , следовательно
, следовательно 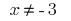 .
. - Нули функции:

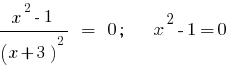
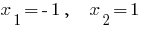
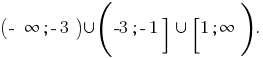
Пример 2.
Указать наименьшее целое число, которое является розвязком неровности
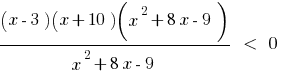
Розвязання. Разрешим данное неравенство методом интервалов.
ОДЗ: 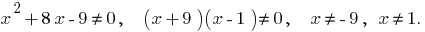
Найдем нули функции: 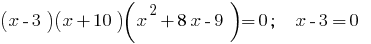 или
или 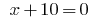
Тогда 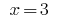 или
или 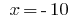 .
.
Изображаем нули и ОДЗ и находим знак функции на каждом промежутке.
Тогда, решение данного неравенства 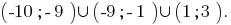 Следовательно, наименьшее целое число, которое является розвязком данного неравенства является число
Следовательно, наименьшее целое число, которое является розвязком данного неравенства является число 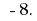
Ответ: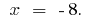


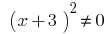 , следовательно
, следовательно 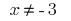 .
.