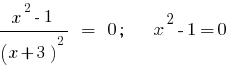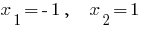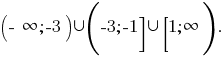Resolver inequações com o равносильных transformação
- A conversão, garantir a conservação correta de igualdade
- Verificação de raízes de substituição original da desigualdade
Solução de equações utilizando o método de intervalos de
- Encontrar ОДЗ.
- Encontrar os zeros da função:

- Notar zeros na ОДЗ e encontrar o sinal da função f(x) em cada período, em que é dividido ОДЗ.
- Anotar a resposta, considerando-se o sinal de um determinado desigualdade.
Resolver inequações. O método de intervalos.
- Encontrar ОДЗ.
- Encontrar os zeros da função:

- Notar zeros na ОДЗ e encontrar o sinal da função f(x) em cada período, em que é dividido ОДЗ.
- Anotar a resposta, considerando-se o sinal de um determinado desigualdade.
Exemplo 1.
Розвяжіть desigualdade: 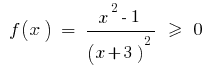
Розвязання. Deixe 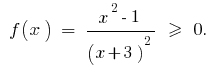
- ОДЗ:
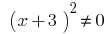 é, portanto
é, portanto 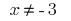 .
. - Zeros de funções:

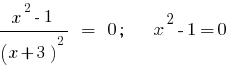
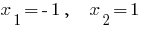
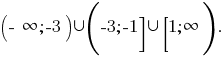
Exemplo 2.
Especificar o menor número inteiro que é розвязком irregularidades
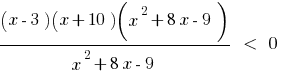
Розвязання. Resolveremos esta desigualdade método de intervalos.
ОДЗ: 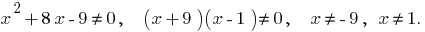
Encontrar os zeros da função: 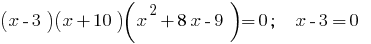 ou
ou 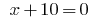
Então 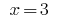 ou
ou 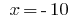 .
.
Representamos os zeros e ОДЗ e encontramos a função sinal em cada período de tempo.
Então, a decisão da desigualdade, 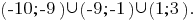 Portanto, o menor número inteiro que é розвязком esta desigualdade é o número de
Portanto, o menor número inteiro que é розвязком esta desigualdade é o número de 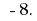
Resposta: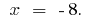


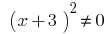 é, portanto
é, portanto 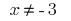 .
.