Função crescente
Definição: uma Função  é chamada de crescente em algum conjunto
é chamada de crescente em algum conjunto 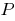 , se o maior valor de um argumento a partir deste conjunto corresponde ao maior valor da função.
, se o maior valor de um argumento a partir deste conjunto corresponde ao maior valor da função.
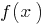 — cresce, se para quaisquer
— cresce, se para quaisquer 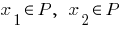
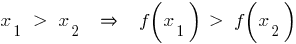
Propriedades crescente em função
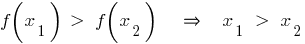
 — função crescente
— função crescente
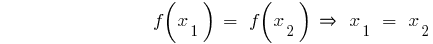 — função crescente
— função crescente
- Se a função
 aumenta em algum conjunto
aumenta em algum conjunto 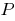 , o maior valor de função corresponde a um valor maior argumento a partir deste conjunto de
, o maior valor de função corresponde a um valor maior argumento a partir deste conjunto de - A soma de vários ascendentes, neste conjunto de funções é o aumento da função neste conjunto.
- Se a função é
 crescente, então a inversa a ela a função também aumenta.
crescente, então a inversa a ela a função também aumenta. - Se em uma função
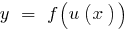 , a função
, a função 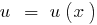 aumenta a função
aumenta a função 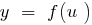 aumenta, então a função
aumenta, então a função 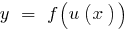 é crescente. O resultado de uma aplicação coerente dois crescentes de funções - função crescente.
é crescente. O resultado de uma aplicação coerente dois crescentes de funções - função crescente. - O resultado de uma aplicação coerente crescente e decrescente, temos a função último.
- Qualquer crescente de um determinado conjunto de função de cada um adquire o seu valor em um ponto apenas do conjunto.
Um sinal de aumento da função de
Se 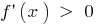 em cada ponto do intervalo
em cada ponto do intervalo  , então a função
, então a função  aumenta no intervalo.
aumenta no intervalo.
Exemplos de funções aumentam em toda a área de definição de
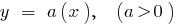
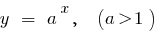
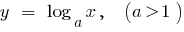
Descendente de função
Definição: uma Função  é chamada de minguante alguma conjunto
é chamada de minguante alguma conjunto 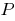 , se o maior valor de um argumento a partir deste conjunto corresponde ao maior valor da função.
, se o maior valor de um argumento a partir deste conjunto corresponde ao maior valor da função.
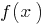 — vem, se para quaisquer
— vem, se para quaisquer 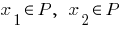
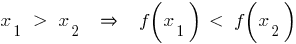
Propriedades de declínio da função
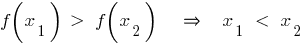
 — último recurso
— último recurso
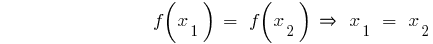 — último recurso
— último recurso
- Se a função
 спадаєна certo conjunto
спадаєна certo conjunto 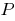 , o maior valor da função corresponde ao menor valor de um argumento a partir deste conjunto de
, o maior valor da função corresponde ao menor valor de um argumento a partir deste conjunto de - A soma de vários descendo neste conjunto de funções é uma função decrescente neste conjunto.
- Se a função é
 decrescente, então a inversa a ela uma característica também diminui.
decrescente, então a inversa a ela uma característica também diminui. - Se em uma função de
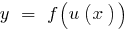 uma função
uma função 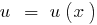 decrescente e função
decrescente e função 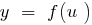 decrescente, função
decrescente, função 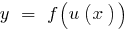 decrescente. O resultado de uma aplicação coerente dois à partida de funções - função crescente.
decrescente. O resultado de uma aplicação coerente dois à partida de funções - função crescente. - O resultado de uma aplicação coerente crescente e decrescente, temos a função último.
- Qualquer descendente de um determinado conjunto de função de cada um adquire o seu valor em um ponto apenas do conjunto.
Sinal de uma função decrescente
Se 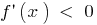 em cada ponto do intervalo
em cada ponto do intervalo  , então a função é
, então a função é  decrescente neste intervalo.
decrescente neste intervalo.
Exemplos de funções, спадающими em toda a área de definição de
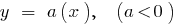
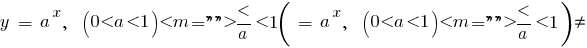
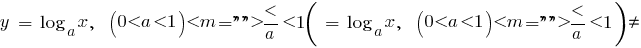

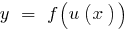 , a função
, a função 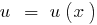 aumenta a função
aumenta a função 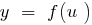 aumenta, então a função
aumenta, então a função