Definição:Se a função 
definida no intervalo 
e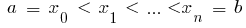 
, em seguida, determinados интегралом da função no intervalo é chamado de número, igual ao limite do montante integral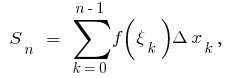 
onde 
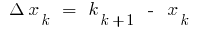, f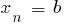 
ou seja,
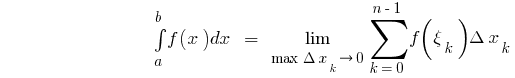
onde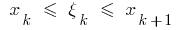 
i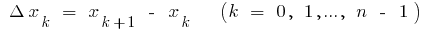 
Construção de um circuito integrado o montante pelo exemplo de determinação da área de curvas linha a
Deixe no intervalo definido неотъемлемою e contínua, a função de
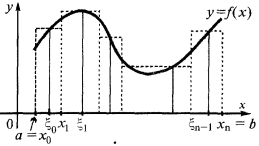
Para determinar o tamanho curvilíneo de um trapézio (limitada a curva de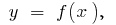 
eixo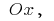 
e direto, 
e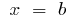 
), dividimos o corte de pontos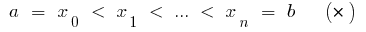 
em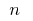 
partes, a escolha de cada uma das derivadas parciais de cortes 
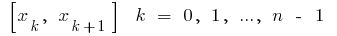ponto arbitrário 
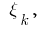calcule o valor
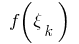da função nesses pontos, e somos a soma 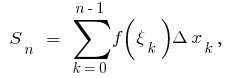de onde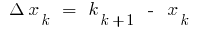
Este valor é igual à soma dos praças sombreadas retângulos e chamado integral do valor.
Agora, se o número de pontos de dividir indefinidamente aumenta e o comprimento máximo (maior) é parcial do corte de dividir tende a zero, e quando este valor 
tende a um limite específico 
, não depende de como particionar 
e escolher os pontos 
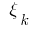em cortes parciais, o valor 
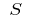é chamado de praça de curvas de trapézio, т. е.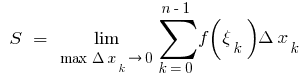 
A Fórmula De Newton - Leibniz
Se a função definida e contínua no segmento de e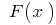 
— sua первообразная (ou seja, 
), 
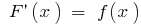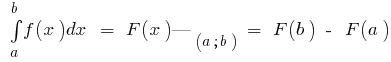
Exemplo. Porque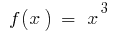 
uma das primitivas, 
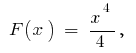o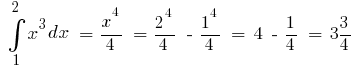 
Principais propriedades da integral definida
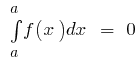
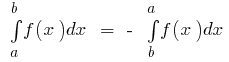
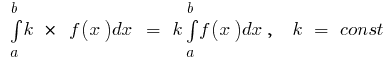
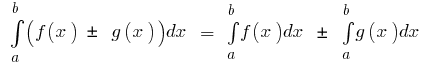
- Se
integrada na 
e 
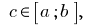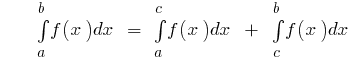
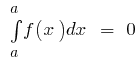
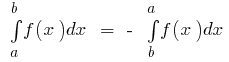
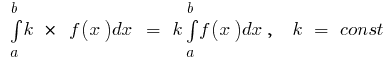
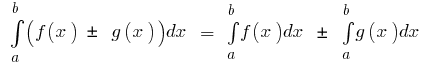
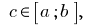o
o