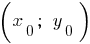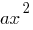Definição: Uma função é chamado de função de tipos 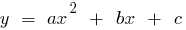 , onde
, onde 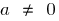
Propriedades de funções quadrática
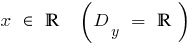
quando 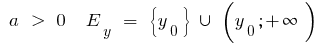
quando 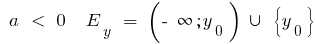
quando a  função nem par nem ímpar
função nem par nem ímpar
quando 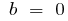 — sala de vapor
— sala de vapor
A função quadrática é contínuo e диференційовна em toda a linha do número, 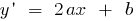
quando 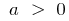 diminui a
diminui a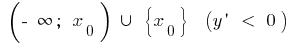 e aumenta
e aumenta 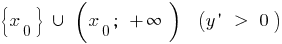 ,
, 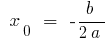 a ponto de mínimo,
a ponto de mínimo, 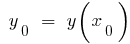 mínimo
mínimo
quando 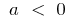 aumenta
aumenta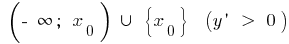 e diminui a
e diminui a 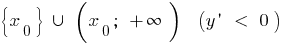 ,
, 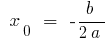 a ponto de máximo,
a ponto de máximo, 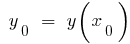 com o máximo de
com o máximo de
As coordenadas do vértice da parábola:
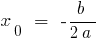 ;
; 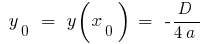 onde
onde 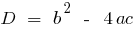
O eixo de simetria da parábola 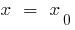
- A definição da área

- Múltiplo do valor

- Paridade, a estranheza
- A continuidade e o дифференцируемость
- Ascendente e descendente, extremos
- Programação quadrática a função é sempre a parábola, ramos, qual é dirigido para cima, com
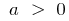 e para baixo quando
e para baixo quando 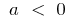
Gráficos de funções quadráticas

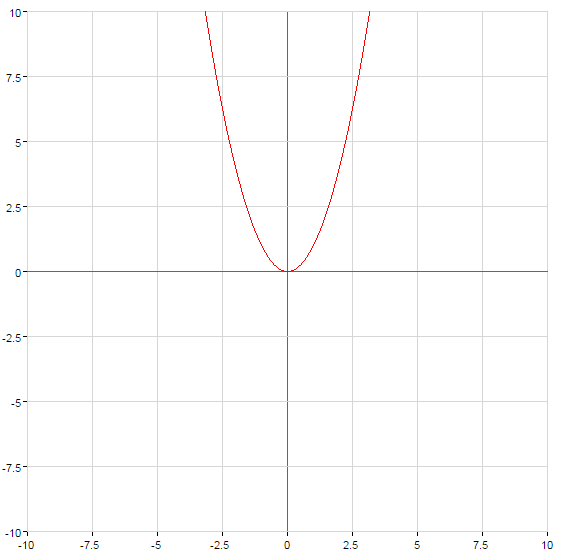

A simetria relativamente ao eixo 
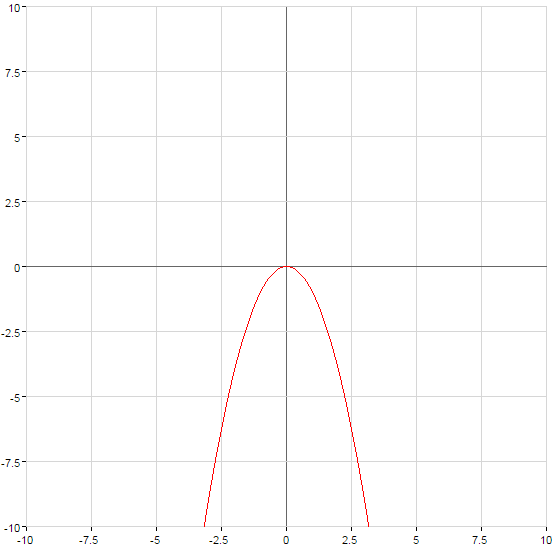

O gráfico da função é comprimido quando 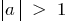 ou esticada quando
ou esticada quando  em um número de unidades igual ao número e
em um número de unidades igual ao número e
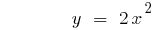
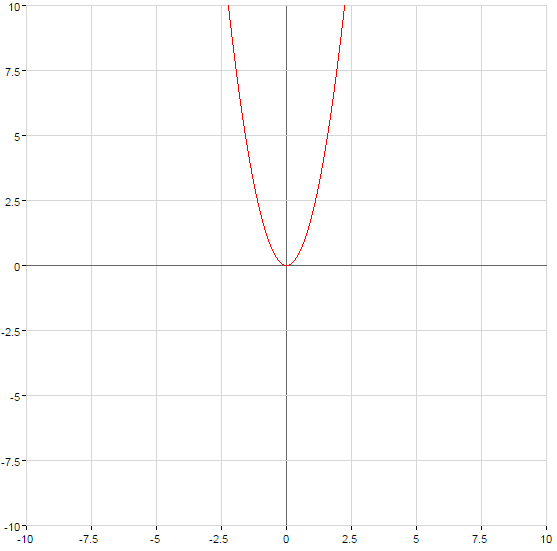
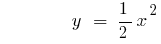
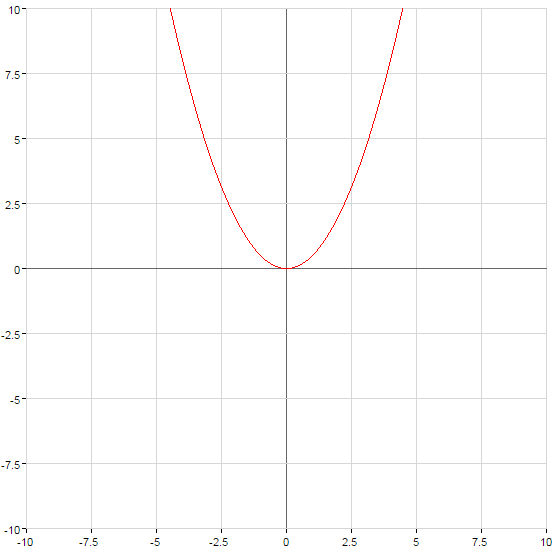
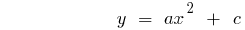
O gráfico da função sobe quando 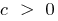 ou desce quando
ou desce quando 
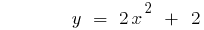
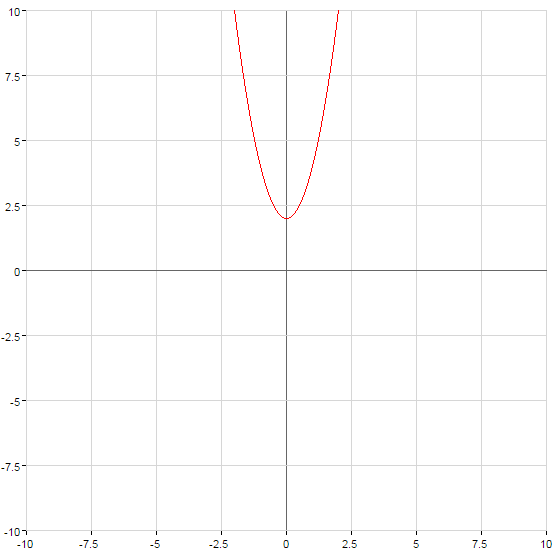
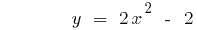
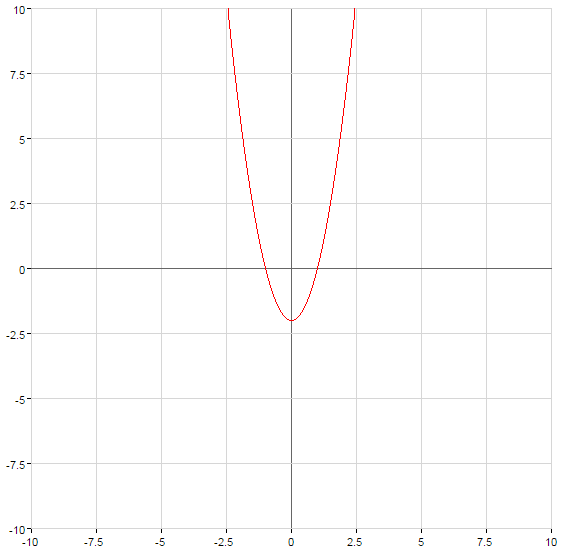
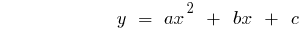
A parábola cruza o eixo  no ponto com
no ponto com
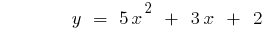
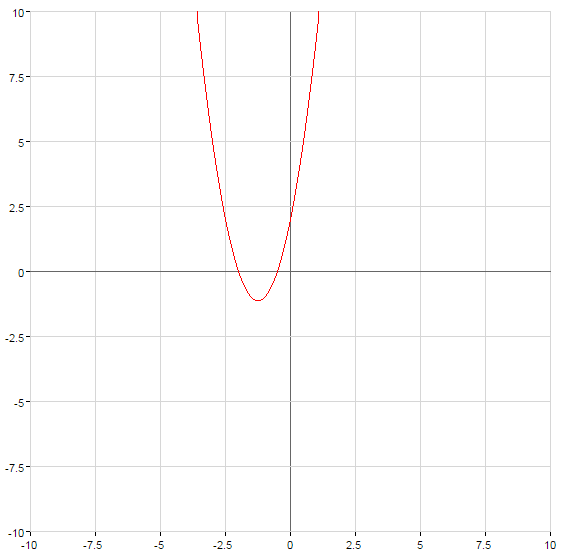
Como construir o gráfico da função quadrática
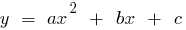
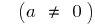
E a maneira de
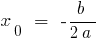
quando os 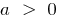 ramos para cima, quando
ramos para cima, quando 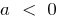 — os galhos para baixo
— os galhos para baixo
- Calcular абсцису topo
- Substituir
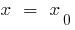 na equação e calcular o ponto em y ao topo
na equação e calcular o ponto em y ao topo 
- Construir um esboço da parábola (tipo
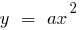 ) com vértice no ponto
) com vértice no ponto 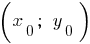
Método II
(ao longo do eixo  a
a 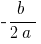 , ao longo do eixo
, ao longo do eixo 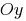 a
a 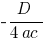 )
)
- Розвязати uma equação quadrática
- Usando transformações elementares de gráficos, executar tradução da parábola
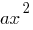




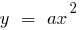 ) com vértice no ponto
) com vértice no ponto