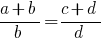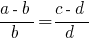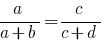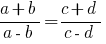A proporção e a relação, directa e de proporcionalidade inversa

Definição: Proporção chamado a igualdade de duas relações.

ou .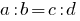

A principal propriedade de proporções

Uma obra de extremo membros membros proporção é igual a obra de suas médias membros: se

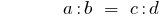, então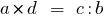

Propriedades de proporções

1. Uma obra de extremo membros membros proporção é igual a obra de suas médias membros: .
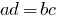2. Cada extremo membro proporção é igual ao produto de suas médias membros, dividido pelo outro extremo membro.
3. Em cada proporção pode trocar ou apenas média membros ou extremo, ou os dois ao mesmo tempo.

Exemplo encontrar a proporção em matemática

Se ,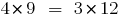

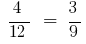
Na proporção de 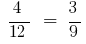mudar os lugares de médias, ou membros de extrema membros, então, temos mais uma vez corretos de igualdad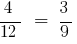e:

e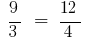

Derivados de taxa de proporção

Se a proporçã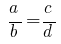o , o 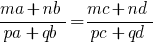que é chamado de derivada de uma proporção.

Mais comuns derivados da proporção

• 
• 
• 
• 

A escala de

Definição: Escala — a relação entre a distância no mapa com a correspondente distância na real do terreno.

Diretamente proporcional a magnitude

Definição: Duas grandezas são chamadas , diretamente пропорциональными, se com o aumento dos valores de uma delas várias vezes o valor de outra aumenta na mesma quantidade de vezes.

Tarefas diretamente proporcionais grandezas

O lado do quadrado é igual a 3 дм. Como mudar o perímetro de um quadrado, se o seu lado de aumentar em 3 vezes, 4 vezes, 5 vezes?

O lado do quadrado de 3 dm, o perímetro de 12 polegada

O lado do quadrado de 9 dm, perímetro 36 dm

O lado do quadrado de 12 polegada, o perímetro de 48 dm

O lado do quadrado de 15 polegada, o perímetro de 60 dm

Ao aumentar o lado de um quadrado em 3 vezes (foi 3 dm, tornou — 9 dm), perímetro aumentou em 3 vezes (foi 9 dm, tornou — 36 dm).

Da mesma forma, quando o aumento do lado do quadrado em 4 vezes (foi 3 dm, tornou — 12 dm), perímetro aumentou em 4 vezes (foi de 12 polegada, tornou — 48 dm).

Conclusão: quando você efetua o lado de um quadrado em várias vezes, o perímetro aumenta em tantas vezes.

O lado do quadrado é diretamente proporcional ao seu perímetro.

São inversamente proporcionais, então

Definição: Duas grandezas são chamadas de обенено пропорциональными, se com o aumento dos valores de uma delas várias vezes o valor da outra diminui na mesma quantidade de vezes.

Tarefas são inversamente proporcionais, então

A distância entre as duas é igual a 160 км. que pode ser acessado a partir de um município para o outro, se a velocidade de 10 km/h aumentar em 2 vezes, 4 vezes, 8 vezes?

Velocidade de km/h 10 h 16

Velocidade de km/h 20 hora h 8

Velocidade de km/h tempo de 40, h 4

Velocidade de km/h 80 tempo, h 2

Quando se aumenta a velocidade em 2 vezes (foi de 10 km/h, tornou-se a 20 km/h), o tempo caiu (caiu) 2 vezes (foi de 16 h, tornou — 8 h).

Da mesma forma, quando se aumenta a velocidade em 4 vezes (foi de 10 km/h, tornou-se a 40 km/h), o tempo caiu (caiu) em 4 vezes (foi de 16 h, tornou — 4 h).

Conclusão: quando se aumenta a velocidade várias vezes, o tempo diminui na mesma quantidade de vezes.

A velocidade é inversamente proporcional ao tempo.

Números 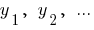proporcionais aos números 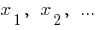, se 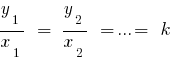— coeficiente de proporcionalidade.
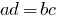