O conceito de irracional equação
Definição: a equação Irracional 
— uma equação que contém a variável sob o signo de raiz -nd.
Solução de equações irracionais
Quando поднесении de ambas as partes da equação ao grau ímpar (1,3,5,7....) obtemos a equação равносильное especificado (no seu ОДЗ)
Exemplo 1:
Розвяжіть equação: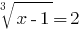 
Solução: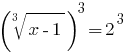 
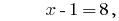
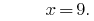
Resposta:
Quando поднесении de ambas as partes da equação em парного степеня (2,4,6,8....) podem receber estranhos raízes, que отсеют verificação.
Exemplo 2:
Розвяжіть equação: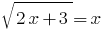 
Solução: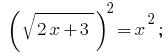 
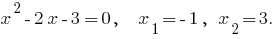
Validação: Quando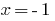 
temos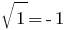 
não é a igualdade, portanto, 
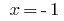- um estranho raiz.
Se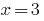 
temos o 
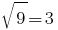(alcorão) é uma igualdade, portanto, 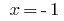é a raiz de um determinado equação.
Resposta: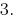
Se na equação a variável faz da mesma forma, o зучно a expressão variável, designado por uma letra do alfabeto (nova variável).
Exemplo 3:
Розвяжіть equação: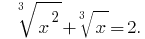 
Solução: Vamos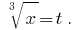 
Então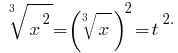 
Obtemos a equação: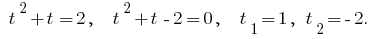 
Executamos a inversa de substituição: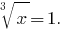 
Então, 
ou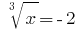 
a partir daqui 
.
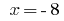Se 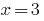temos o 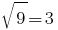(alcorão) é uma igualdade, portanto, 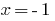é a raiz de um determinado equação.
Resposta: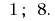
- Com a ajuda da elevação de ambas as partes da equação irracional a um grau de
- Com a substituição de variáveis