A monotonia e a constância da função
Uma condição crescente de funções
Se em cada ponto do intervalo 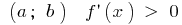 , então a função aumenta no intervalo de
, então a função aumenta no intervalo de
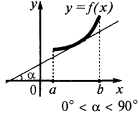
Condição suficiente decrescente, de acordo com a função
Se em cada ponto do intervalo 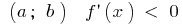 , então a função é decrescente neste intervalo de
, então a função é decrescente neste intervalo de
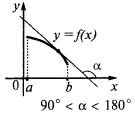
A observação. Estes termos e condições são apenas suficientes, mas não são necessárias condições de crescimento e função decrescente
Condição necessária e suficiente de permanência função
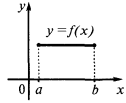
A função  é constante no intervalo de
é constante no intervalo de 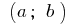 então, e só então, quando
então, e só então, quando  todos os pontos do intervalo todo
todos os pontos do intervalo todo
Extremos (máximos e mínimos) da função
O ponto de máximo
Definição: um Ponto  do domínio da função
do domínio da função  é chamado de ponto de máximo desta função, se houver
é chamado de ponto de máximo desta função, se houver 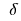 - bairro
- bairro 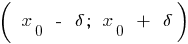 ponto
ponto  , que, para todos,
, que, para todos, 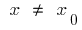 a partir deste bairro é executado a desigualdade
a partir deste bairro é executado a desigualdade 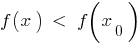
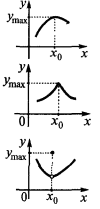
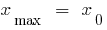 — ponto de máximo
— ponto de máximo
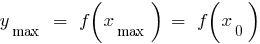 — máximo de
— máximo de
O ponto de mínimo
Definição: um Ponto  do domínio da função
do domínio da função  é chamado de ponto de mínimo desta função, se houver
é chamado de ponto de mínimo desta função, se houver 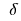 - bairro
- bairro 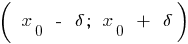 ponto
ponto  , que, para todos,
, que, para todos, 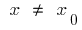 a partir deste bairro é executado a desigualdade
a partir deste bairro é executado a desigualdade 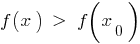
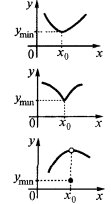
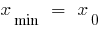 — ponto de mínimo
— ponto de mínimo
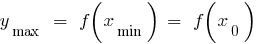 — mínimo de
— mínimo de
Ponto crítico
Definição: Internos ponto de escopo de função, em que a derivada de uma função é igual a zero ou de não existir são chamados de críticos
A condição necessária extrema
 — o ponto extremo
— o ponto extremo 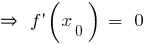 ou
ou 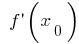 não existe
não existe
(mas não em cada ponto  , onde
, onde 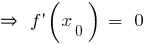 ou
ou 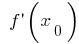 não existir, será exagerado!)
não existir, será exagerado!)
Uma condição extrema
no ponto de  sinal
sinal 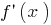 muda com
muda com 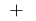 o
o 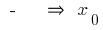 ponto de máximo
ponto de máximo
no ponto de  sinal
sinal 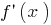 muda com
muda com 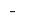 o
o 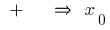 ponto de mínimo
ponto de mínimo
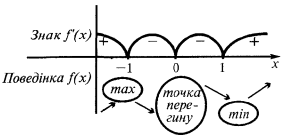
Um exemplo de gráficos de funções  , que tem extremos
, que tem extremos
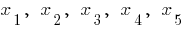 — ponto crítico
— ponto crítico
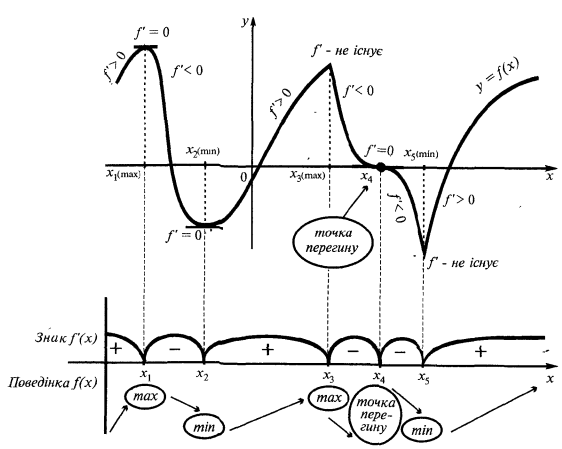
A função de pesquisa sobre a monotonia e extremos
Exemplo. 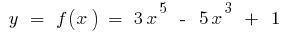
A definição da área: 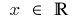
Função contínua em cada ponto de sua área de definição
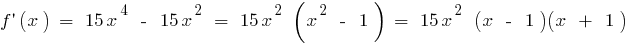
 há em toda a área de definição de
há em toda a área de definição de
 quando
quando 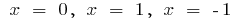
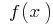 aumenta quando
aumenta quando 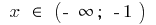 e quando
e quando 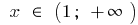
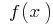 diminui quando
diminui quando 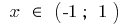
Do ponto de extremum: 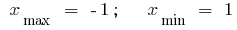
Extremos: 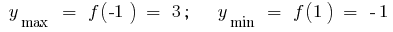
- Encontrar a definição da área e os intervalos em que a função é contínua
- Para encontrar a derivada

- Localizar os pontos críticos, т. е. internos de um ponto de definição de área, em que
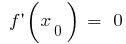 ou não existe
ou não existe - Marcar os pontos críticos na definição de área, encontrar o sinal da função derivada e a descrição do comportamento da função em cada intervalo, em que é dividida a área de detecção de
- Relativamente a cada ponto crítico determinar se ela é o ponto de máximo ou mínimo ou não é um ponto de extrema
- Gravar потріний o resultado de um estudo (em intervalos de monotonia e extremos)
O maior e o menor valor de função contínua no intervalo
Propriedade: Se a função  é contínua em um intervalo fechado e tem nele um número finito de pontos críticos, ela adquire o seu maior e o menor valor neste segmento, ou em pontos críticos, pertença a esta corte, ou nas extremidades do corte
é contínua em um intervalo fechado e tem nele um número finito de pontos críticos, ela adquire o seu maior e o menor valor neste segmento, ou em pontos críticos, pertença a esta corte, ou nas extremidades do corte
Encontrar o maior e o menor valor da função contínua no intervalo
Exemplo. 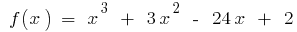 quando
quando 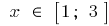
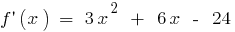
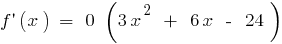 se
se 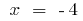 e quando
e quando 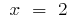
A um determinado segmento 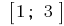 pertence somente a um ponto crítico
pertence somente a um ponto crítico 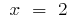
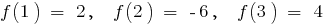

- Para encontrar a derivada

- Localizar os pontos críticos (
 ou não existe)
ou não existe) - Escolher o ponto crítico, que pertencem a um determinado segmento
- Calcular o valor da função em pontos críticos e nas extremidades do corte
- Comparar os valores obtidos e escolher o menor e o maior

 , que tem extremos
, que tem extremos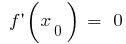 ou não existe
ou não existe