Монотонність і сталість функції
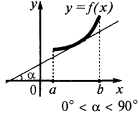
Достатня умова зростання функції
Якщо в кожній точці інтервалу 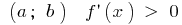 , то функція зростає на цьому інтервалі
, то функція зростає на цьому інтервалі
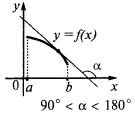
Достатня умова спадання функції
Якщо в кожній точці інтервалу 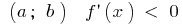 , то функція спадає на цьому інтервалі
, то функція спадає на цьому інтервалі
Зауваження. Ці умови є лише достатніми, але не є необхідними умовами зростання і спадання функції
Необхідна і достатня умова сталості функції
Функція  є сталою на інтервалі
є сталою на інтервалі 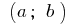 тоді і тільки тоді, коли
тоді і тільки тоді, коли  в усіх точках уього інтервалу
в усіх точках уього інтервалу
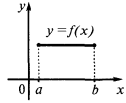
Екстремуми (максимуми і мінімуми) функції
Точка максимуму
Означення: Точка  з області визначення функції
з області визначення функції  називається точкою максимуму цієї функції, якщо знайдеться
називається точкою максимуму цієї функції, якщо знайдеться 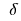 - окіл
- окіл 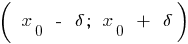 точки
точки  , такий, що для всіх
, такий, що для всіх 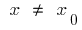 з цього околу виконується нерівність
з цього околу виконується нерівність 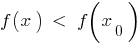
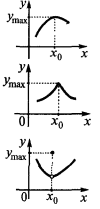
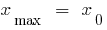 — точка максимуму
— точка максимуму
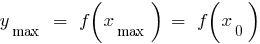 — максимум
— максимум
Точка мінімуму
Означення: Точка  з області визначення функції
з області визначення функції  називається точкою мінімуму цієї функції, якщо знайдеться
називається точкою мінімуму цієї функції, якщо знайдеться 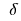 - окіл
- окіл 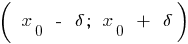 точки
точки  , такий, що для всіх
, такий, що для всіх 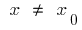 з цього околу виконується нерівність
з цього околу виконується нерівність 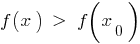
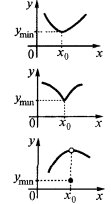
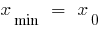 — точка мінімуму
— точка мінімуму
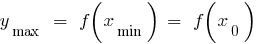 — мінімум
— мінімум
Критичні точки
Означення: Внутрішні точки області визначення функції, в яких похідна функції дорівнює нулю або не існує, називаються критичними
Необхідна умова екстремуму
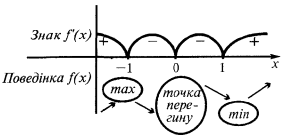
 — точка екстремуму
— точка екстремуму 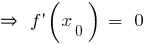 або
або 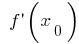 — не існує
— не існує
(але не в кожній точці  , де
, де 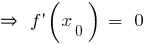 або
або 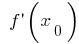 не існує, буде екстремум!)
не існує, буде екстремум!)
Достатня умова екстремуму
у точці  знак
знак 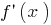 змінюється з
змінюється з 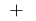 на
на 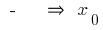 — точка максимуму
— точка максимуму
у точці  знак
знак 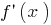 змінюється з
змінюється з 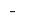 на
на 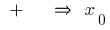 — точка мінімуму
— точка мінімуму
Приклад графіка функції  , що має екстремуми
, що має екстремуми
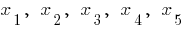 — критичні точки
— критичні точки
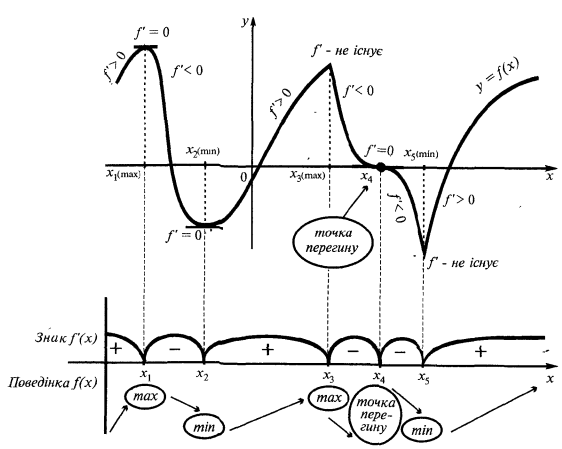
Дослідження функції на монотонність і екстремуми
Приклад. 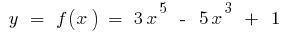
Область визначення: 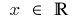
Функція неперервна в кожній точці своєї області визначення
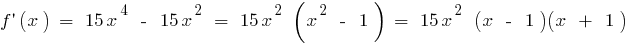
 існує на всій області визначення
існує на всій області визначення
 при
при 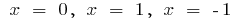
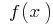 зростає при
зростає при 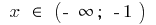 і при
і при 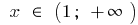
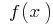 спадає при
спадає при 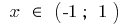
Точки екстремуму: 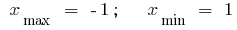
Екстремуми: 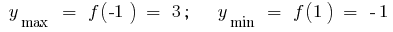
- Знайти область визначення і інтервали, на яких функція неперервна
- Знайти похідну

- Знайти критичні точки, тобто внутрішні точки області визначення, в яких
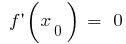 або не існує
або не існує - Позначити критичні точки на області визначення, знайти знак похідної і характер поведінки функції на кожному інтервалі, на які розбивається область визначення
- Відносно кожної критичної точки визначити, чи є вона точкою максимуму або мінімуму, чи не є точкою екстремуму
- Записати потріний результат дослідження (проміжки монотонності і екстремуми)
Найбільше і найменше значення функції, неперервної на відрізку
Властивість: Якщо функція  неперервна на відрізку і має на ньому скінченне число критичних точок, то вона набуває свого найбільшого і найменшого значення на цьому відрізку або в критичних точках, які належать цьому відрізку, або на кінцях відрізка
неперервна на відрізку і має на ньому скінченне число критичних точок, то вона набуває свого найбільшого і найменшого значення на цьому відрізку або в критичних точках, які належать цьому відрізку, або на кінцях відрізка
Знаходження найбільшого і найменшого значення функції, неперервної на відрізку
Приклад. 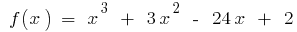 при
при 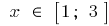
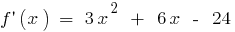
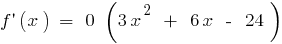 при
при 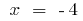 і при
і при 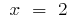
Заданому відрізку 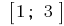 належить лише критична точка
належить лише критична точка 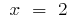
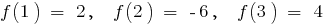

- Знайти похідну

- Знайти критичні точки (
 або не існує)
або не існує) - Вибрати критичні точки, які належать заданому відрізку
- Обчислити значення функції в критичних точках і на кінцях відрізку
- Порівняти одержані значення і вибрати з них найменше і найбільше

 , що має екстремуми
, що має екстремуми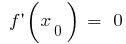 або не існує
або не існує