Означення: Число 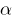 називається коренем многочлена
називається коренем многочлена  , якщо
, якщо 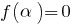 (тобто
(тобто 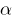 є коренем рівняння
є коренем рівняння  )
)
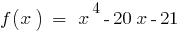 . Число 3 — корінь многочлена, оскільки
. Число 3 — корінь многочлена, оскільки 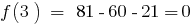
Найпростіші властивості коренів
Оскільки 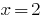 — корінь многочлена
— корінь многочлена 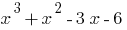 , то цей многочлен ділиться на
, то цей многочлен ділиться на 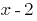 ;
;
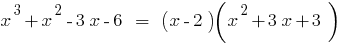
- Якщо число
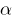 є коренем многочлена
є коренем многочлена  , то цей многочлен ділиться на двочлен
, то цей многочлен ділиться на двочлен 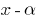 без остачі — наслідок з теореми Безу;
без остачі — наслідок з теореми Безу; - Многочлен степеня
 може мати не більше
може мати не більше  коренів;
коренів; - Якщо для многочлена
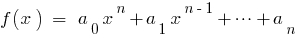 ит знаємо
ит знаємо  його коренів:
його коренів: 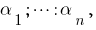 то цей многочлен можна розкласти на множники так:
то цей многочлен можна розкласти на множники так: 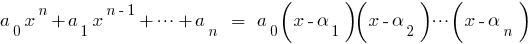 .
.
Формули Вієта
Якщо 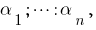 — корені многочлена
— корені многочлена 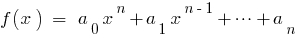 то порівнюючи коефіцієнти при однакових степенях
то порівнюючи коефіцієнти при однакових степенях  ліворуч і праворуч, одержуємо співвідношення між коренями многочлена та його коефіцієнтами, які називаються формули Вієти.
ліворуч і праворуч, одержуємо співвідношення між коренями многочлена та його коефіцієнтами, які називаються формули Вієти.
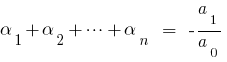
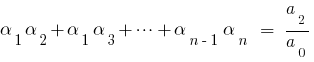
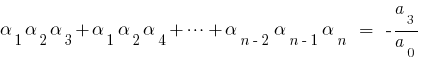
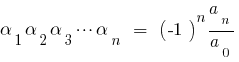
При 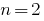 для квадратного тричлена
для квадратного тричлена 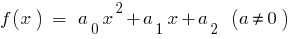 маємо
маємо
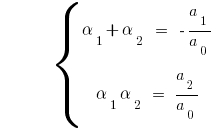
При 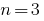 для кубічного тричлена
для кубічного тричлена 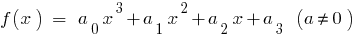 маємо
маємо
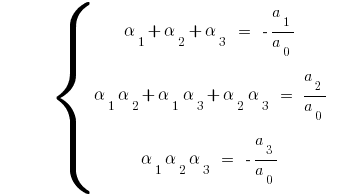

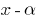 без остачі — наслідок з
без остачі — наслідок з  може мати не більше
може мати не більше 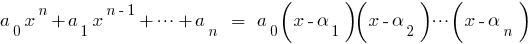 .
.