Означення: Многочленом від однієї змінної  — многочлен вигляду
— многочлен вигляду 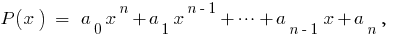 де
де 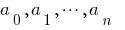 — числові коефіцієнти.
— числові коефіцієнти.
Означення: Якщо 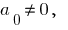 то цей многочлен називається многочленом
то цей многочлен називається многочленом  -ого степеня відносно змінної
-ого степеня відносно змінної  .
.
Член 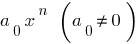 називається старшим членом многочлена
називається старшим членом многочлена 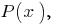 a
a 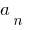 — його вільним членом.
— його вільним членом.
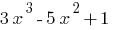 — многочлен третього степеня.
— многочлен третього степеня.
Тотожно рівні многочлени від однієї змінної
Означення: Два многочлена називаються тотожно рівними, якщо вони набувають рівних значень при всіх значеннях змінної.
Властивості тотожної рівності многочленів від однієї змінної
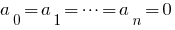
- Якщо многочлен
 тотожно дорівнює нулю (тобто набуває нульових значень при усіх значеннях
тотожно дорівнює нулю (тобто набуває нульових значень при усіх значеннях  ), то всі його коефіцієнти дорівнюють нулю.
), то всі його коефіцієнти дорівнюють нулю. - Якщо два многочлена
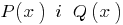 тотожно рівні (тобто набувають однакових значень при усіх значеннях
тотожно рівні (тобто набувають однакових значень при усіх значеннях  ), то вони збігаються (тобто їх степеня однакові і коефіцієнти при однакових степенях рівні).
), то вони збігаються (тобто їх степеня однакові і коефіцієнти при однакових степенях рівні).
Ділення многочлена на многочлен
Означення: Якщо для двох многочленів 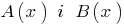 можна знайти такий многочлен
можна знайти такий многочлен 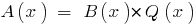 , то говорять, що
, то говорять, що 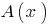 ділиться на
ділиться на  .
.
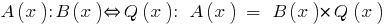
Приклад
Оскільки, 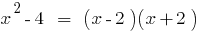 , то многочлен
, то многочлен 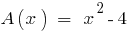 ділиться на многочлен
ділиться на многочлен 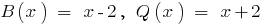
Ділення многочлена на многочлен з остачею
Означення: Многочлен 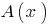 ділиться на многочлен
ділиться на многочлен  з остачею, якщо можна знайти пару многочленів
з остачею, якщо можна знайти пару многочленів 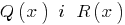 , що
, що 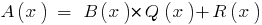 , причому степінь остачі
, причому степінь остачі 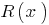 менший від степеня
менший від степеня  .
.
Якщо остача 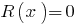 , то многочлен
, то многочлен 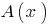 ділиться на многочлен
ділиться на многочлен  (без остачі)
(без остачі)
Приклад
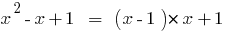
,
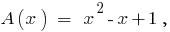
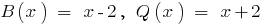
Ділення многочлена на многочлен "куточком"
Правило ділення многочленів від однієї змінної
- Розмістити члени многочленів за спадними степенями змінної.
- Поділити старший член діленого на старший член дільника.
- Одержаний результат помножити на дільник і цей добуток відняти від діленого.
- З одержаною різницею виконують аналогічну операцію: ділять її старший член на старший член дільника і здобутий результат знов множать на дільник і так далі. Цей процес продовжують дати, доки не одержать в остачі нуль (якщо один многочлен ділиться на другий) або поки в остачі не одержать многочлен, степінь якого менший від степеня дільника.
Теорема Безу
Остача від ділення многочлена  на двочлен
на двочлен 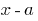 дорівнює
дорівнює 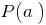
Наслідок: Якщо 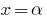 — корінь многочлена
— корінь многочлена  (тобто
(тобто 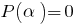 ), то цей многочлен ділиться без остачі на
), то цей многочлен ділиться без остачі на 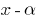 .
.
Приклад
Остача від ділення многочлена 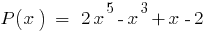 на двочлен
на двочлен 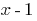 дорівнює
дорівнює 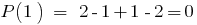 , тобто
, тобто  ділиться на
ділиться на 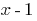 без остачі.
без остачі.
Поділивши  на
на 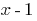 "куточком" або за схемою Горнера, одержуємо:
"куточком" або за схемою Горнера, одержуємо: 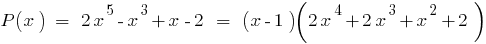

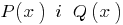 тотожно рівні (тобто набувають однакових значень при усіх значеннях
тотожно рівні (тобто набувають однакових значень при усіх значеннях