Зростаюча функція
Означення: Функція  називається зростаючою на деякій множині
називається зростаючою на деякій множині 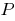 , якщо більшому значенню аргументу з цієї множини відповідає більше значення функції.
, якщо більшому значенню аргументу з цієї множини відповідає більше значення функції.
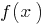 — зростає, якщо для будь яких
— зростає, якщо для будь яких 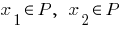
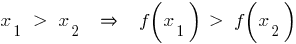
Властивості зростаючої функції
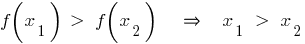
 — зростаюча функція
— зростаюча функція
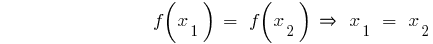 — зростаюча функція
— зростаюча функція
- Якщо функція
 зростає на деякій множині
зростає на деякій множині 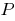 , то більшому значенню функції відповідає більше значення аргументу з цієї множини
, то більшому значенню функції відповідає більше значення аргументу з цієї множини - Сума кількох зростаючих на даній множині функцій є зростаючою функцією на цій множині.
- Якщо функція
 зростає, то обернена до неї функція також зростає.
зростає, то обернена до неї функція також зростає. - Якщо у складеній функції
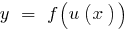 функція
функція 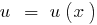 зростає і функція
зростає і функція 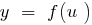 зростає, то і функція
зростає, то і функція 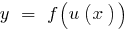 зростає. Результат послідовного застосування двох зростаючих функцій - зростаюча функція.
зростає. Результат послідовного застосування двох зростаючих функцій - зростаюча функція. - Результат послідовного застосування зростаючої і спадної функції є функція спадна.
- Будь-яка зростаюча на заданій множині функція набуває кожного свого значення лише в одній точці з цієї множини.
Ознака зростання функції
Якщо 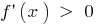 в кожній точці інтервалу
в кожній точці інтервалу  , то функція
, то функція  зростає на цьому інтервалі.
зростає на цьому інтервалі.
Приклади функцій, що зростають на всій області визначення
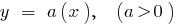
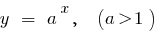
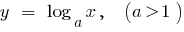
Спадна функція
Означення: Функція  називається спадною на деякій множині
називається спадною на деякій множині 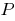 , якщо більшому значенню аргументу з цієї множини відповідає більше значення функції.
, якщо більшому значенню аргументу з цієї множини відповідає більше значення функції.
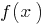 — спадає, якщо для будь яких
— спадає, якщо для будь яких 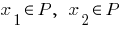
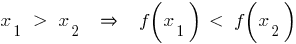
Властивості спадної функції
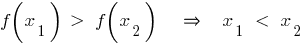
 — спадна функція
— спадна функція
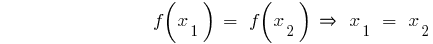 — спадна функція
— спадна функція
- Якщо функція
 спадаєна деякій множині
спадаєна деякій множині 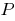 , то більшому значенню функції відповідає менше значення аргументу з цієї множини
, то більшому значенню функції відповідає менше значення аргументу з цієї множини - Сума кількох спадних на даній множині функцій є спадною функцією на цій множині.
- Якщо функція
 спадає, то обернена до неї функція також спадає.
спадає, то обернена до неї функція також спадає. - Якщо у складеній функції
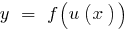 функція
функція 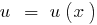 спадає і функція
спадає і функція 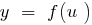 спадає, то і функція
спадає, то і функція 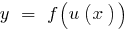 спадає. Результат послідовного застосування двох спадних функцій - зростаюча функція.
спадає. Результат послідовного застосування двох спадних функцій - зростаюча функція. - Результат послідовного застосування зростаючої і спадної функції є функція спадна.
- Будь-яка спадна на заданій множині функція набуває кожного свого значення лише в одній точці з цієї множини.
Ознака спадання функції
Якщо 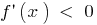 в кожній точці інтервалу
в кожній точці інтервалу  , то функція
, то функція  спадає на цьому інтервалі.
спадає на цьому інтервалі.
Приклади функцій, що спадають на всій області визначення
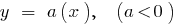
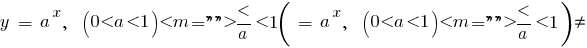
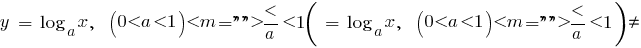

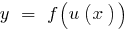 функція
функція 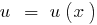 зростає і функція
зростає і функція 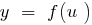 зростає, то і функція
зростає, то і функція