Системи нерівностей, розвязування систем лінійних нерівностей

Поняття системи та її розвязків

Означення: Якщо ставиться завдання знайти всі спільні розвязки двох (або більше) нерівностей з однією або кількома змінними, то кажуть, що треба розвязати систему нерівностей.

Означення: Розвязком системи — таке значення змінної або такий упорядкований набір значень зміниих, що задовольняє одразу всім нерівностям системи, тобто розвязком системи двох або більше нерівностей з невідомими називається така упорядкована множина множина з чисел, при підстановці яких у систему замість невідомих усі нерівності перетворюються на правильні числові рівності.

Означення: Розвязати систему рівнянь — знайти всі її розвязки або довести, що їх немає.

Якщо система не має розвязку, то вона є несумісна.

Приклад систем нерівностей

 

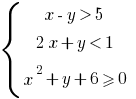— система трьох рівнянь з двома змінними

Пара 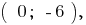тобто 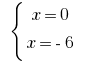— один із розвязків системи

Схема розвязування систем нерівностей з однією змінною

1. Розвязуємо кожну нерівність окремо.
2. Знайти всі спільні розвязки даних нерівностей.

Схема розвязування систем нерівностей з декілька змінними

1. Розвязуємо систему нерівностей, як систему рівнянь, помінявши, на деякий час, знак нерівності на знак рівності.
2. Поміняти знак назад та знайти всі спільні розвязки даних нерівностей.

Приклади розвязування систем рівнянь

 

Розвязування графічним методом

Приклад 1

Розвяжіть рівняння: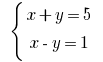

Розвязання:

Будуємо графіки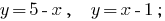

Побудувавши графіки побачимо, що графіки перетинаються в точці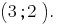

Відповідь: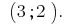

 

Розвязування методом підстановки

Приклад 2

Розвяжіть рівняння: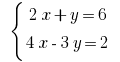

Розвязання:

З першого рівняння виражаємо 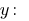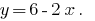А одержаний вираз підставляємо в друге рівняння системи:

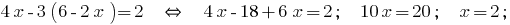
Одержане значення підставляємо у вираз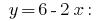

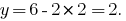
Відповідь: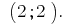

 

Розвязування методом додавання

Приклад 3

Розвяжіть рівняння: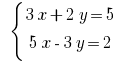

Розвязання:

Маємо позбутись змінної 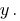Множимо почленно перше рівняння системи на 3, а друге – на 2.

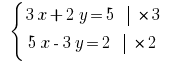
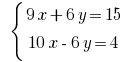
Додаємо почленно рівняння і одержуємо: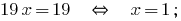

Знаходимо значення з першого рівняння системи: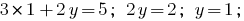

Відповідь: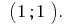

 

Зауваження: В методі додавання можна множити не тільки на додатні числа, а і на відємні.

Яким способом розвязувати систему рівнянь вирішувати тільки Вам.