Означення: Лінійною функцією називають функцію вигляду  , де
, де 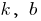 — деякі числа
— деякі числа
Властивості лінійних функцій
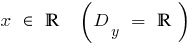
при 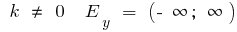
при 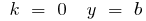
при 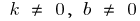 — функція ні парна, ні непарна
— функція ні парна, ні непарна
при 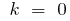 — парна
— парна
при 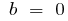 і
і 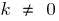 — непарна
— непарна
при 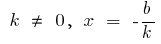 — точка перетину з віссю
— точка перетину з віссю 
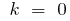 , тоді
, тоді 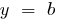 — пряма, яка паралельна осі
— пряма, яка паралельна осі  при
при 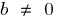 і збігається з віссю
і збігається з віссю  при
при 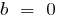
Лінійна функція неперервна і диференційовна на всій числовій прямій 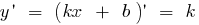
при 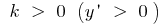 функція зростає на всій числовій прямій
функція зростає на всій числовій прямій
при 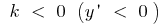 функція спадає на всій числовій прямій
функція спадає на всій числовій прямій
при 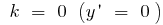 функція стала
функція стала
- Область визначення

- Множина значення

- Парність, непарність
- Точки перетину з осями координат
- Неперервність і диференційовність
- Зростання і спадання
- Графіком лінійної функції завжди є пряма, тангенс кута нахилу цієї прямої до осі
при
 - точка перетину з віссю
- точка перетину з віссю 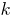
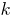 — кутовий коефіцієнт прямої
— кутовий коефіцієнт прямої 
при
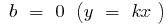 — пряма, що проходить через початок координат
— пряма, що проходить через початок координатпри
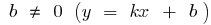 — пряма, що не проходить через початок координат
— пряма, що не проходить через початок координат
Графіки лінійних функцій
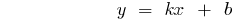
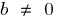
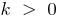
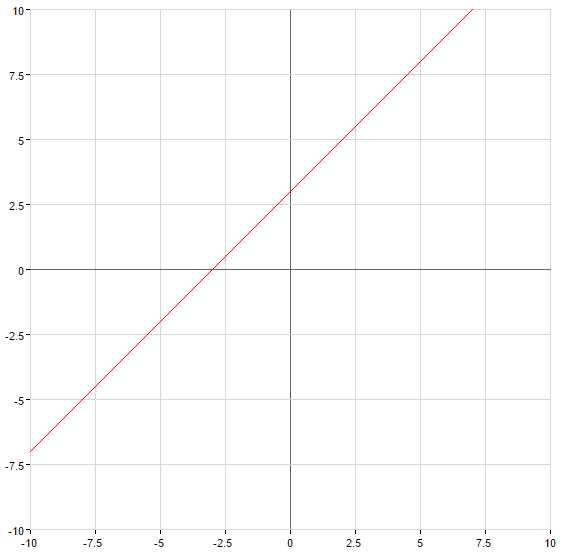
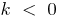
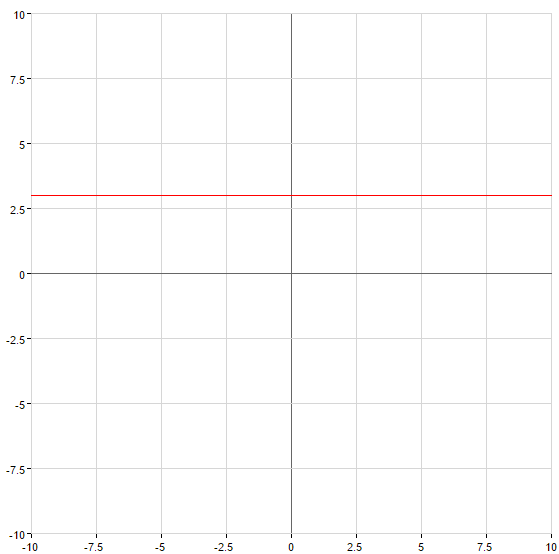
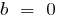
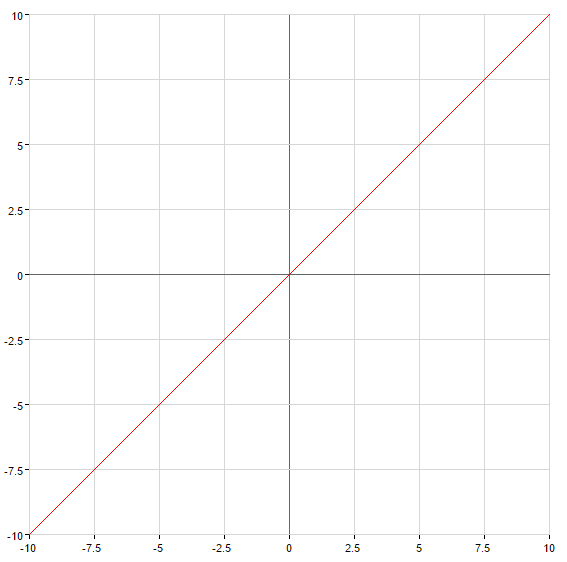



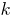
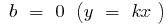 — пряма, що проходить через початок координат
— пряма, що проходить через початок координат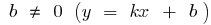 — пряма, що не проходить через початок координат
— пряма, що не проходить через початок координат