Означення: Функція вигляду 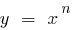 , де n — будь-яке дійсне число, називається степеневою функцією
, де n — будь-яке дійсне число, називається степеневою функцією
Властивості степеневої функції (при 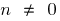 )
)
a) n — натуральне  b) n — ціле відємне
b) n — ціле відємне  c) n — не ціле
c) n — не ціле
a)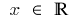
b)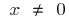
c) при 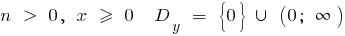
 при
при 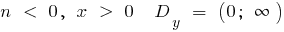
a) при n парному 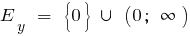
 при n непарному
при n непарному 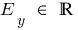
b) при n парному 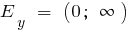
 при n непарному
при n непарному 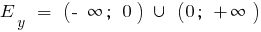
c) при 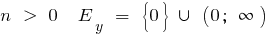
 при
при 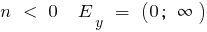
a),b) при n парному — парна
 при n непарному — непарна
при n непарному — непарна
c) ні парна, ні непарна
не періодична
a) 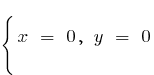
b) немає
c) при 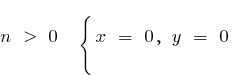
 при
при  — немає
— немає
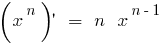
a) при n парному 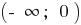 — спадає,
— спадає,  — зростає
— зростає
 при n непарному — зростає
при n непарному — зростає
b) при n парному 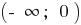 — зростає,
— зростає,  — спадає
— спадає
 при n непарному
при n непарному 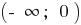 — спадає,
— спадає,  — спадає
— спадає
c) при 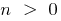 — зростає
— зростає
 при
при  — спадає
— спадає
a) при n парному 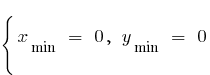
 при n непарному — немає
при n непарному — немає
b) немає
c) при 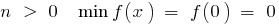
 при
при 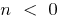 — немає
— немає
a) немає
b) 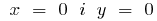
c) при 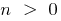 — немає
— немає
 при
при 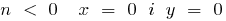
a) при n парному  — опуклість вниз
— опуклість вниз
 при n непарному,
при n непарному, 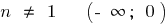 —
— 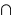 ;
;  —
—  ; 0 — точка перегину
; 0 — точка перегину
b) при n парному — 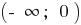 —
—  ;
;  —
— 
 при n непарному —
при n непарному — 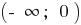 —
— 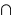 ;
;  —
— 
c) при 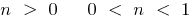 —
— 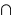 ;
; 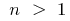 —
— 
 при
при 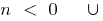
Якщо 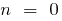 , то
, то 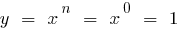 (при
(при 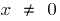 )
)
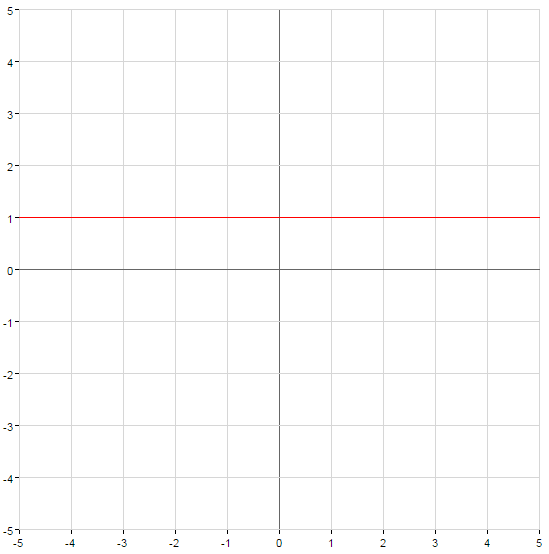
- Область визначення

- Множина значення

- Парність, непарність
- Періодичність
- Перетин з осями координат
- Похідна
- Зростання і спадання
- Екстремуми
- Асимптоти
- Опуклість та точки перегину
- Особливий випадок
Графіки степеневих функцій

- n — парне натуральне число
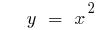
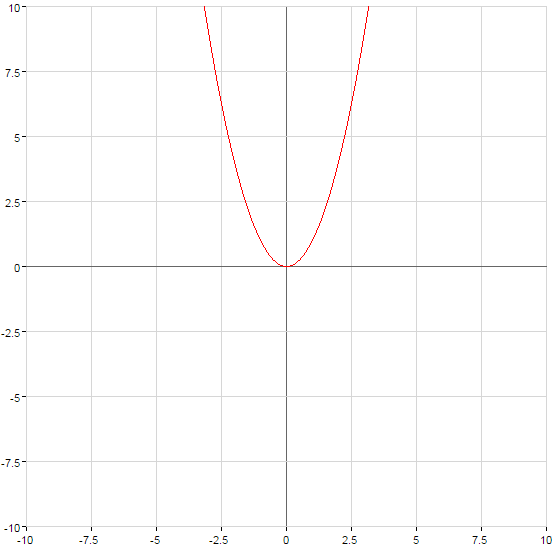
- n — непарне натуральне число
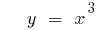
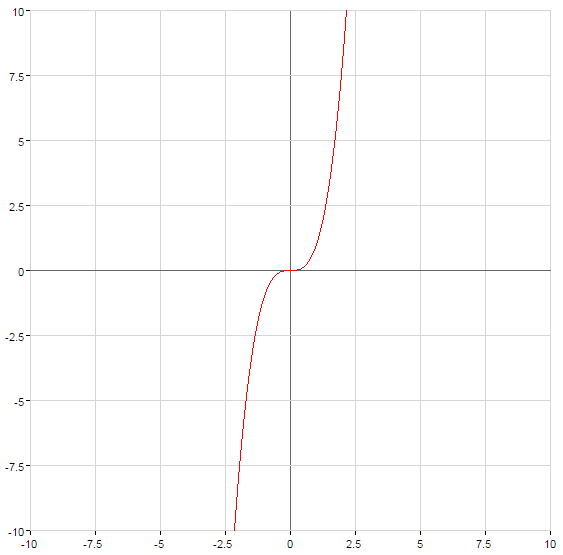
- n — непарне відємне число
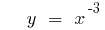
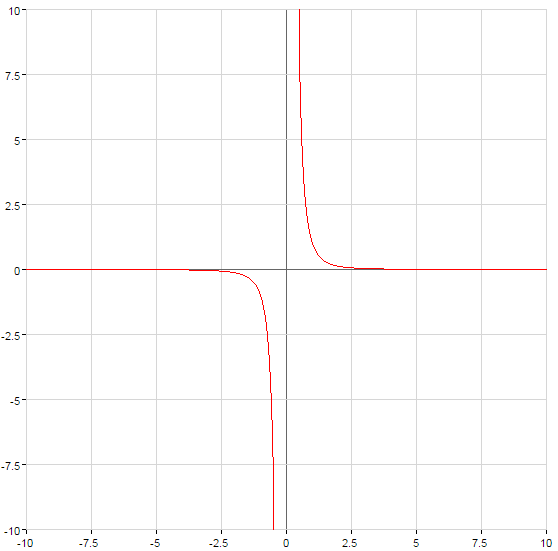
- n — парне відємне число
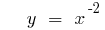
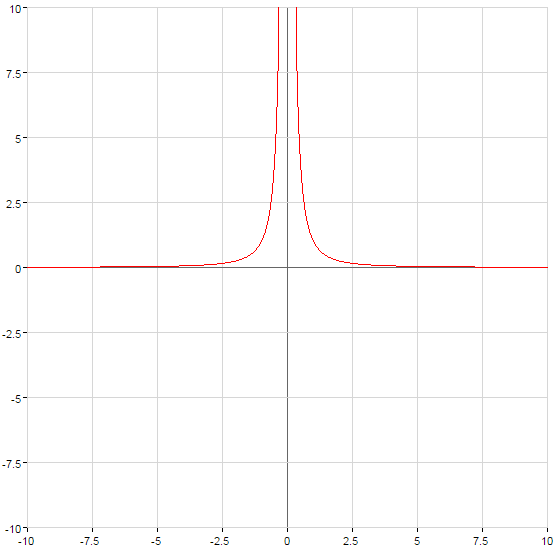
- n — не ціле додатнє число
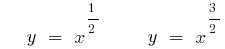 (зелений)
(зелений)
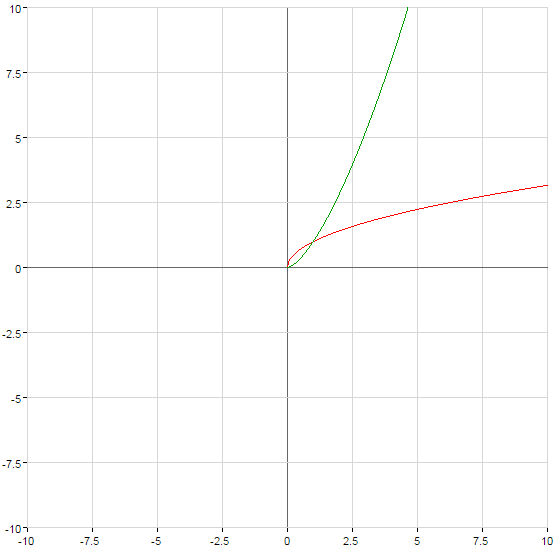
- n — не ціле відємне число
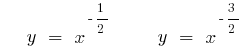 (зелений)
(зелений)
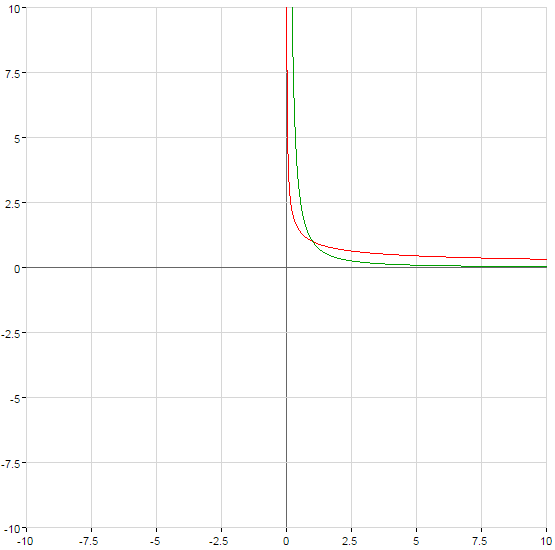

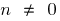 )
)
