Определение: Функция вида 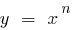 , где n — любое действительное число, называется степенной функцией
, где n — любое действительное число, называется степенной функцией
Свойства степенной функции (при 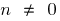 )
)
a) n — натуральное  b) n — целое відємне
b) n — целое відємне  c) n — не целое
c) n — не целое
- Область определения

- Множественное значение

- Четность, нечетность
- Периодичность
- Пересечение с осями координат
- Производная
- Возрастание и убывание
- Экстремумы
- Асимптоты
- Выпуклость и точки перегиба
- Особый случай
a)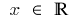
b)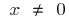
c) при 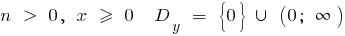
 при
при 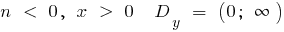
a) при n парном 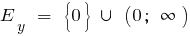
 при n нечетном
при n нечетном 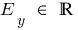
b) при n парном 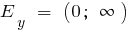
 при n нечетном
при n нечетном 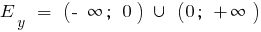
c) при 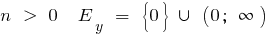
 при
при 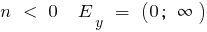
a),b) при n парном — парная
 при n нечетном — нечетное
при n нечетном — нечетное
c) ни четная, ни нечетная
не периодическая
a) 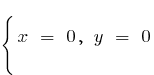
b) нет
c) при 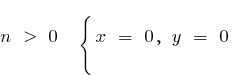
 при
при  — нет
— нет
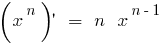
a) при n парном 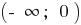 — убывает,
— убывает,  — возрастает
— возрастает
 при n нечетном — растет
при n нечетном — растет
b) при n парном 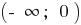 — возрастает,
— возрастает,  — убывает
— убывает
 при n нечетном
при n нечетном 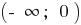 — приходит,
— приходит,  — приходит
— приходит
c) при 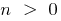 — растет
— растет
 при
при  — приходит
— приходит
a) при n парном 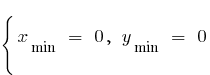
 при n нечетном — нет
при n нечетном — нет
b) нет
c) при 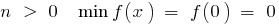
 при
при 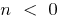 — нет
— нет
a) нет
b) 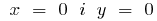
c) при 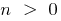 — нет
— нет
 при
при 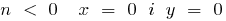
a) при n парном  — выпуклость вниз
— выпуклость вниз
 при n нечетном,
при n нечетном, 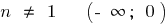 —
— 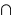 ;
;  —
—  ; 0 — точка перегиба
; 0 — точка перегиба
b) при n парном — 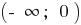 —
—  ;
;  —
— 
 при n нечетном —
при n нечетном — 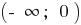 —
— 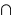 ;
;  —
— 
c) при 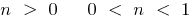 —
— 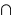 ;
; 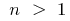 —
— 
 при
при 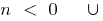
Если 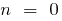 , то
, то 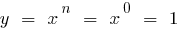 (при
(при 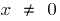 )
)
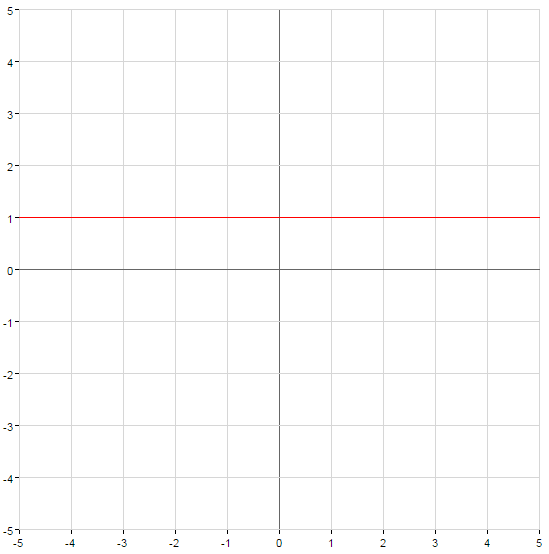
Графики степенных функций

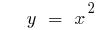
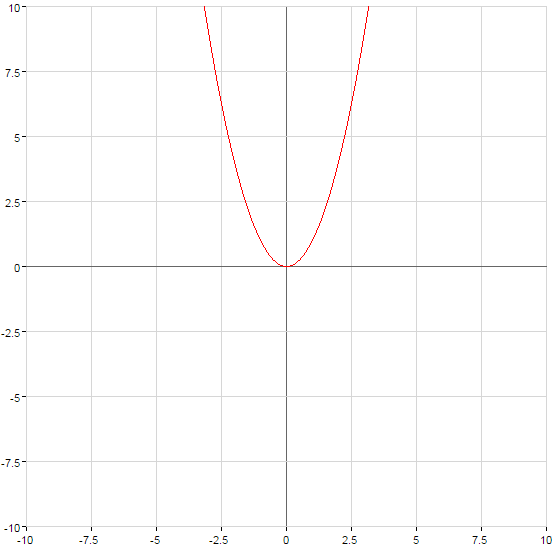
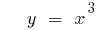
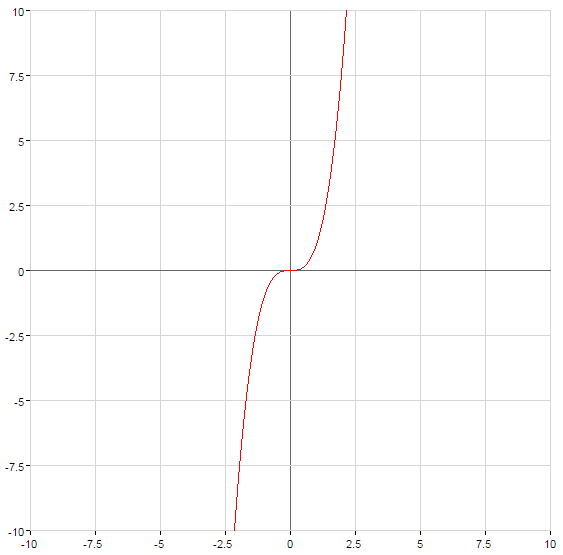
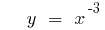
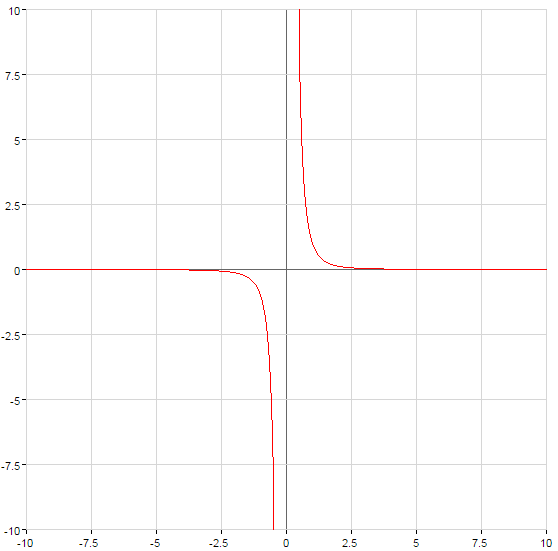
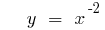
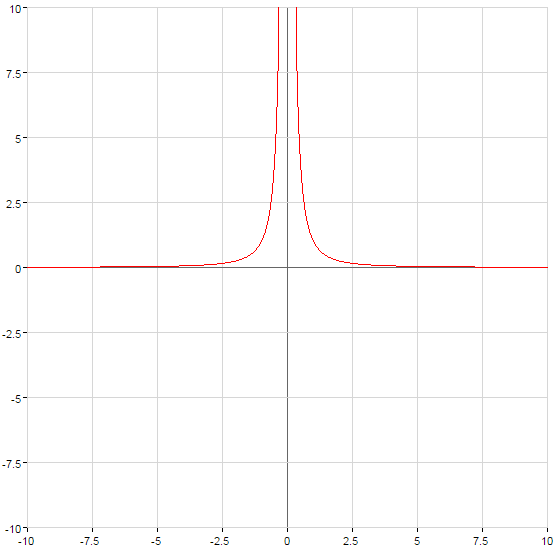
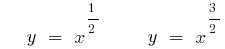 (зеленый)
(зеленый)
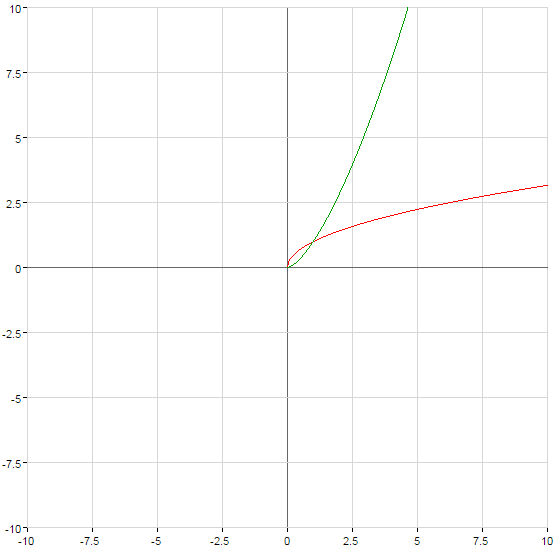
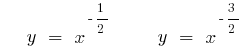 (зеленый)
(зеленый)
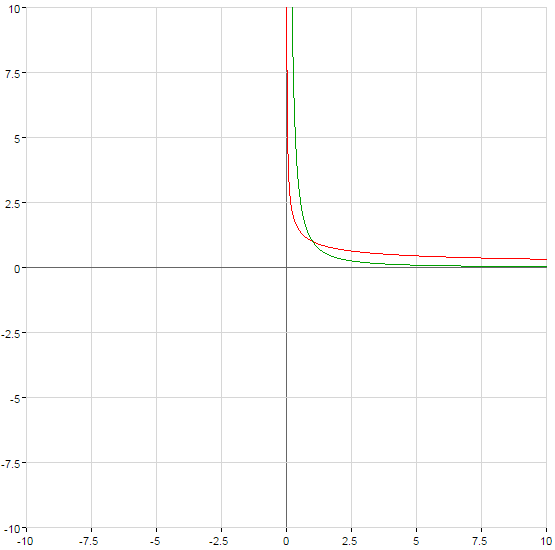

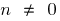 )
)
