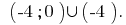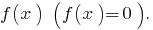Понятие иррационального неравенства
Определение: Иррациональное неравенство  — неравенство, содержащее переменную под знаком корня
— неравенство, содержащее переменную под знаком корня  -ой степени.
-ой степени.
Решению иррациональных уравнений
Метод интервалов для решению иррациональных неравенств
- Найти ОДЗ неравенства.
- Найти нули функции
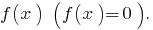
- Отменить нули функции на ОДЗ и найти знак функции на каждом из промежутков, на которые разбивается ОДЗ .
Пример 1:
Розвяжіть уравнения: 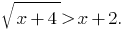
Решение: Заданное неравенство равносильно неравенству 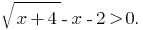
Обозначим 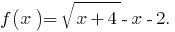
ОДЗ: 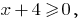 , т. е.
, т. е. 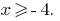
Нули: 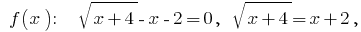 подносим в квадрат левую и правую часть
подносим в квадрат левую и правую часть 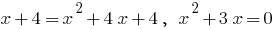
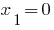 - корень,
- корень, 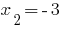 - посторонний корень.
- посторонний корень.
Ответ: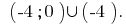
Равносильные преобразования
- При поднесении обеих частей неравенства до нечетного степень (с сохранением знака неравенства) получаем неравенство, равносильное данному.
- Если обе части неравенства невідємні, то при подъеме обеих частей неравенства к парному степени (с сохранением знаком неравенства) получаем неравенство, равносильное данному.
- Если на ОДЗ заданного неравенства какая-то часть неравенства может приобретать как положительные, так и неотъемлемых значений, то, прежде чем подносить обе части неравенства до парного степеня, эти случаи стоит рассмотреть отдельно.
Пример 2:
Розвяжіть уравнения: 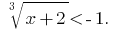
Решение: ОДЗ: 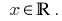
Заданное неравенство равносильно неравенствам: 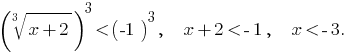
Ответ: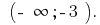
Пример 3 :
Розвяжіть уравнения: 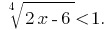
Решение: ОДЗ: 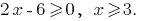
Обе части заданного неравенства невідємні, следовательно, она равносильно неравенствам: 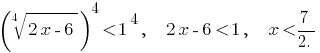
Учитывая ОДЗ, получаем 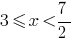 .
.
Ответ: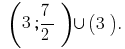
Пример 4 :
Розвяжіть уравнения: 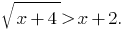
Решение: Заданное неравенство равносильно совокупности систем:
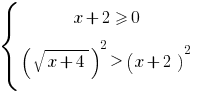 или
или 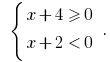
Тогда 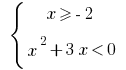 или
или 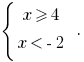
Розвязавши неравенство 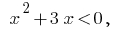 имеем
имеем 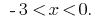
Учитывая неравенство 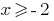 , получаем решение первой системы
, получаем решение первой системы 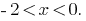 . Решение второй системы:
. Решение второй системы: 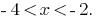 Обєднуючи эти развязки, получаем ответ.
Обєднуючи эти развязки, получаем ответ.
Ответ: