Квадратное уравнение, теорема Виета

Квадратные уравнения

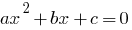Определение: Квадратное уравнение — уравнение вида , где 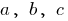— некоторые числа, причем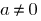

Квадратное уравнение общего вида

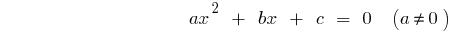
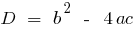— дискриминантов квадратного уравнения

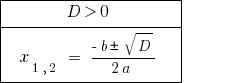
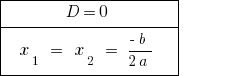
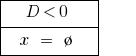
При 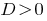— уравнение имеет два различных корня.

При — уравнение имеет два равных корня. При подсчете количества розвязків считается одно значение корня.

При 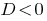— уравнение корней нет.

Сводное уравнение (а = 1)

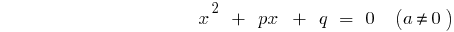
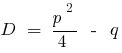— дискриминантов сводного уравнения

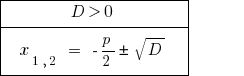
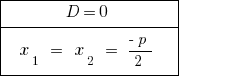
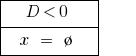
При 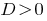— сводное уравнение имеет два различных корня.

При — сводное уравнение имеет два равных корня. При подсчете количества розвязків считается одно значение корня.

При 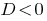— сводное уравнения корней нет.

Теорема Виета в общем случае

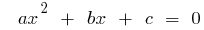Если — корни квадратного уравнения , то

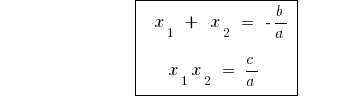
Теорема Виета для сводного уравнение (a=1)

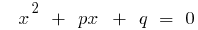Если — корни сводного квадратного уравнения , то

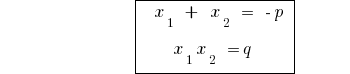
Обратная теорема теореме Виета

Теорема: Если сумма двух чисел равна 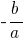, а произведение равно 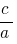, то эти числа являются корнями квадратного уравнения .

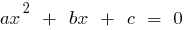Теорема (для сводного уравнения): Если сумма двух чисел равна 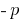, а произведение равно 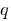, то эти числа являются корнями квадратного уравнения .

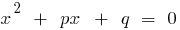Разложение квадратного трехчлена на множители

Если — корни квадратного трехчлена равен нулю 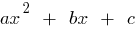(то есть корни уравнения 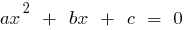), то

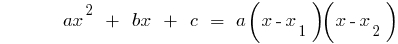
Если дискриминантов квадратного трехчлена равен нулю (), то 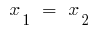, и тогда

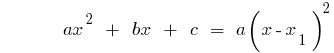
Пример. Разложение трехчлена на множители

1. при



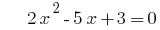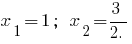
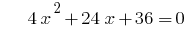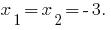
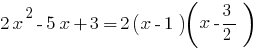
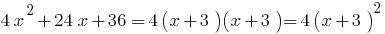
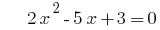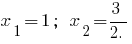
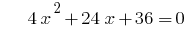2. при