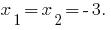দ্বিঘাত সমীকরণ
সংজ্ঞা: দ্বিঘাত সমীকরণ 
— একটি সমীকরণ ফর্ম 
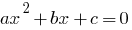যেখানে 
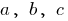কিছু সংখ্যা, এবং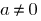 
দ্বিঘাত সমীকরণের সাধারণ ফর্ম
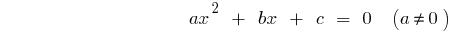
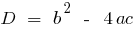— এই discriminants এর দ্বিঘাত সমীকরণ
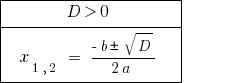
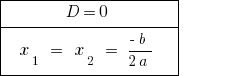
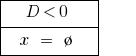
যদি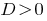 
সমীকরণ আছে দুটি স্বতন্ত্র শিকড়.
যদি 
সমীকরণ দুটি সমান শিকড়. যখন বেড়ে চলেছে, সংখ্যা rozwaski এক বিবেচনা করা হয় মান রুট.
যখন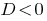 
— সমীকরণ শিকড় আছে.
মাস্টার সমীকরণ (একটি = 1)
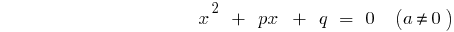
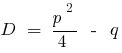— এই discriminants এর মিলিত সমীকরণ
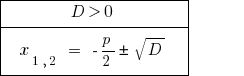
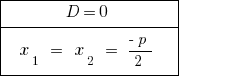
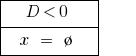
এ 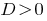— মাস্টার সমীকরণ আছে দুটি স্বতন্ত্র শিকড়.
যখন — সমীকরণ দুটি সমান শিকড়. যখন বেড়ে চলেছে, সংখ্যা rozwaski এক বিবেচনা করা হয় মান রুট.
যদি 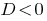— সমীকরণ শিকড় আছে না.
Vieta উপপাদ্য সাধারণ ক্ষেত্রে
যদি 
শিকড় দ্বিঘাত সমীকরণ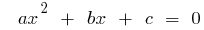 
, তারপর
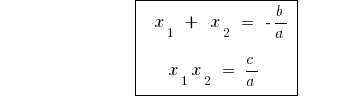
এই vieta উপপাদ্য জন্য মাস্টার সমীকরণ (একটি=1)
যদি একত্রীকৃত শিকড় এর দ্বিঘাত সমীকরণ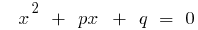 
, তারপর
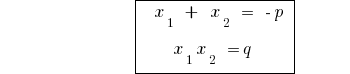
বিপরীত উপপাদ্য উপপাদ্য এর vieta
উপপাদ্য: যদি যোগফল দুই সংখ্যার সমান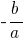 
, এবং পণ্য এখনও 
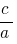, এই সংখ্যা হয়, এর শিকড় দ্বিঘাত সমীকরণ 
.
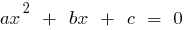উপপাদ্য (মাস্টার সমীকরণ): যদি যোগফল দুই সংখ্যার সমান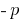 
, এবং পণ্য এখনও 
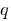, এই সংখ্যা হয়, এর শিকড় দ্বিঘাত সমীকরণ 
.
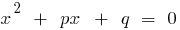পচানি একটি বর্গক্ষেত্র trinomial মধ্যে কারণের
যদি শিকড় দ্বিঘাত trinomial শূন্য সমান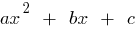 
(অর্থাৎ শিকড় সমীকরণ 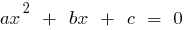), তারপর
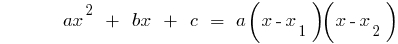
যদি discriminants স্কয়ার trinomial সমান শূন্য (), 
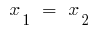এবং তারপর
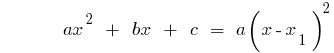
উদাহরণ. পচানি trinomial.
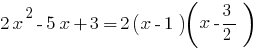
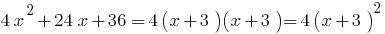
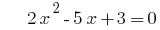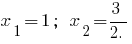
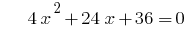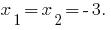
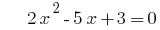যখন 
যখন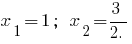 
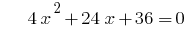যখন 
যখন 