মূল
সংজ্ঞা: একটি ফাংশন 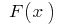 বলা হয়, প্রাথমিক ফাংশন
বলা হয়, প্রাথমিক ফাংশন  উপর এই ব্যবধান, যদি থাকে,
উপর এই ব্যবধান, যদি থাকে,  এই সময়ের
এই সময়ের 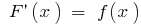
উদাহরণ
- জন্য ফাংশন
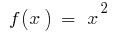 ব্যবধান
ব্যবধান 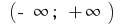 প্রাথমিক হয়
প্রাথমিক হয় 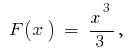 , কারণ
, কারণ 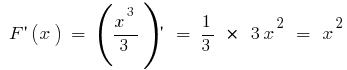
- জন্য ফাংশন
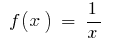 ব্যবধান
ব্যবধান 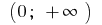 প্রাথমিক হয়
প্রাথমিক হয় 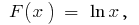 , কারণ
, কারণ 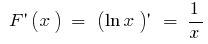
প্রধান সম্পত্তি অবিচ্ছেদ্য
যদি কাজ 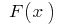 হয়, প্রাথমিক ফাংশন
হয়, প্রাথমিক ফাংশন  উপর এই ব্যবধান, এবং
উপর এই ব্যবধান, এবং 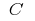 একটি অবাধ, ধ্রুবক, ফাংশন
একটি অবাধ, ধ্রুবক, ফাংশন 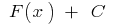 এছাড়াও প্রাথমিক ফাংশন
এছাড়াও প্রাথমিক ফাংশন 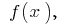 এই ক্ষেত্রে, কোন আদিম ফাংশন
এই ক্ষেত্রে, কোন আদিম ফাংশন  উপর এই ব্যবধান হতে পারে আকারে লেখা
উপর এই ব্যবধান হতে পারে আকারে লেখা 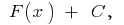 যেখানে
যেখানে 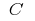 একটি অবাধ ওঠে
একটি অবাধ ওঠে
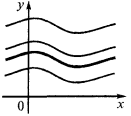
জ্যামিতিক অর্থ
কোন গ্রাফিক্স আদিম এই ফাংশন থেকে প্রাপ্ত করা যাবে দ্বারা একে অপরের সমান্তরাল স্থানান্তর অক্ষ বরাবর 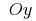
অনির্দিষ্ট সমাকলন
সংজ্ঞা:এই সেট এর সব প্রিমিটিভের এর একটি প্রদত্ত ফাংশন  বলা হয় এবং অনির্দিষ্ট সমাকলন এবং দ্বারা সূচিত করা হয়,
বলা হয় এবং অনির্দিষ্ট সমাকলন এবং দ্বারা সূচিত করা হয়, 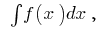 অর্থাত্
অর্থাত্ 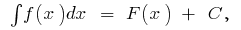 যেখানে
যেখানে 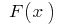 এক আদিম ফাংশন
এক আদিম ফাংশন 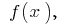 এবং
এবং 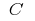 কিছু হয়ে ওঠে
কিছু হয়ে ওঠে
নিয়ম ইন্টিগ্রেশন
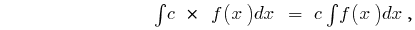 যেখানে
যেখানে 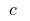 হয়ে ওঠে
হয়ে ওঠে
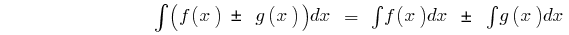
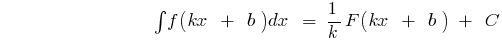

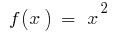 ব্যবধান
ব্যবধান 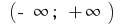 প্রাথমিক হয়
প্রাথমিক হয় 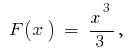 , কারণ
, কারণ 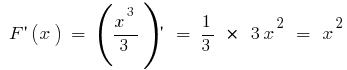
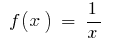 ব্যবধান
ব্যবধান 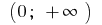 প্রাথমিক হয়
প্রাথমিক হয় 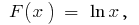 , কারণ
, কারণ