সংজ্ঞা: একটি সমীকরণ এক পরিবর্তনশীল 
হয়, সমতা সঙ্গে একটি পরিবর্তনশীল 
, যা সাধারণ ফর্ম ভালো লেখা হয়: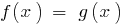 
সংজ্ঞা: একটি রুট (বা rozvyazka) সমীকরণ বলা হয়, মান পরিবর্তনশীল করে তোলে যে সমীকরণ সত্য সংখ্যাসূচক সমতার.
Razvesti সমীকরণ মানে খোঁজার সব তার শিকড় (interchanges) বা দেখানোর জন্য যে, তারা না হয়.
এলাকার সম্ভবপর মান (odz) সমীকরণ
সংজ্ঞা: এলাকায় অনুমোদিত মান (পরিসীমা সংজ্ঞা) এর সমীকরণ — সার্বিক সুযোগ জন্য ফাংশন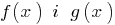 
দাঁড়িয়ে, বাম এবং ডান অংশ সমীকরণ.
এটি এলাকার সম্ভবপর মান (odz)
উদাহরণ
সেট সমীকরণ: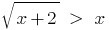 
DHS: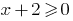 
অর্থাৎ 
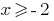, যেমন ডোমেইন এর ফাংশন 
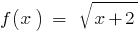দ্বারা নির্ধারিত হয়, শর্ত 
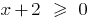, এবং ডোমেইন এর ফাংশন 
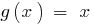সেট করা হয় সব বাস্তব সংখ্যা.
সমীকরণ — তদন্ত
যদি প্রতিটি রুট এর প্রথম সমীকরণ root-র দ্বিতীয় সমীকরণ, দ্বিতীয় সমীকরণ বলা হয়, এর ফলে প্রথম সমীকরণ.
যদি বৈধতা প্রথম সমতা মানেই শুদ্ধতা প্রতিটি নিম্নলিখিত তাহলে adejumo সমীকরণ একটি ফল
অতএব, যখন, ব্যবহার, সমীকরণ এবং প্রভাব যাচাই, শিকড় দ্বারা প্রতিস্থাপন মূল সমীকরণ একটি অংশ সমাধান.
উদাহরণ 1
Razvesti সমীকরণ: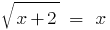 
সমাধান:
আসুন নির্মাণ উভয় অংশের সমীকরণ মধ্যে একটি বর্গক্ষেত্র:
;
;
;
.
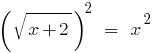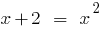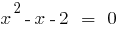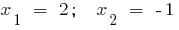কি একটি ব্যাকগ্রাউন্ড চেক.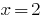 
— root-র 
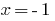বাইরে হয় রুট.
উত্তর: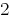 
.
সমতুল্য সমীকরণ
সংজ্ঞা: সমতুল্য (সমতুল্য) সমীকরণ — দুটি সমীকরণ, যার জন্য অনেক DHS আছে একই ফলাফল যে হয়, প্রতিটি সমাধান এর প্রথম সমীকরণ হয় rozvyazka দ্বিতীয়, এবং তদ্বিপরীত.
কিছু উপপাদ্য সম্পর্কে সমানভাবে প্রভাবশালী হয় সমীকরণ
উপপাদ্য 1: যদি এক অংশ সমীকরণ থেকে সরাতে আরেকটি অংশ, পদ সঙ্গে বিপরীত সাইন, আমরা একটি পেতে সমীকরণ সমতুল্য একটি দেওয়া (কোন সেট).
উপপাদ্য 2: যদি উভয় অংশের সমীকরণ হবে, গুন বা ভাগ দ্বারা একই সংখ্যা শূন্যের সমান না (বা এক এবং একই ফাংশন যে সংজ্ঞায়িত করা হয় এবং শূন্যের সমান না করে আইডি দেওয়া সমীকরণ), আমরা পেতে সমীকরণ সমতুল্য দেওয়া এক.
উপপাদ্য 3: যদি উভয় অংশের সমীকরণ 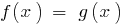নিতে একটি ক্রমবর্ধমান (বা সাজানো) ফাংশন 
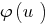এবং না vdbase সংকীর্ণ আইডি দেওয়া সমীকরণ 
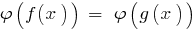হবে, সমতুল্য একটি প্রদত্ত ( DHS).
Corollaries এর উপপাদ্য সম্পর্কে সমানভাবে প্রভাবশালী হয় সমীকরণ
ফল: কারণ ফাংশন হয়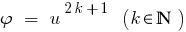 
monotonically বৃদ্ধি,তারপর
.
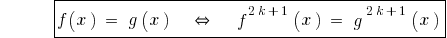উপস্থাপনা উভয় অংশের সমীকরণ মধ্যে অদ্ভুত প্রাকৃতিক ডিগ্রী, ফলে সমীকরণ সমতূল্য এই.
ফল: কারণ ফাংশন হয়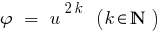 
monotonically বৃদ্ধি শুধুমাত্র যদি 
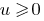ক্ষেত্রে,যখন উভয় অংশের সমীকরণ newmn, উদ্ধরণ দ্বারা উভয় অংশ, এমনকি প্রাকৃতিক ডিগ্রী, ফলে সমীকরণ সমতূল্য এই.