সীমা ফাংশন এ অসীম

সংজ্ঞা: যাক একটি ফাংশন সংজ্ঞায়িত সমগ্র নম্বর লাইন. সংখ্যা 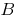বলা হয়, সীমা ফাংশন , এ 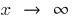জন্য যদি কোন 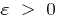অস্তিত্ব আছে একটি সংখ্যা 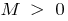জন্য যে সব সন্তোষজনক অবস্থা 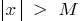, নিম্নলিখিত বৈষম্য সন্তুষ্ট হয়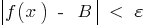

তাহলে 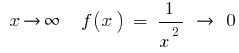, যে, জন্য বড় (পরম) এর মান সংখ্যা 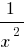খুব সামান্য থেকে ভিন্ন, সংখ্যা 0

 

যদি এই আচরণ করা হয়, বিভিন্ন সঙ্গে 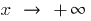এবং 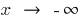আলাদাভাবে বিবেচনা 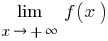(সংজ্ঞা গ্রহণ 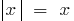) এবং 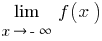(সংজ্ঞা নিন )

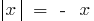সীমা একটি ক্রম

যেহেতু একটি অনুক্রম হল একটি ফাংশন, প্রাকৃতিক যুক্তি 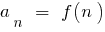সংজ্ঞা সীমা একটি ক্রম সঙ্গে 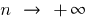অভিন্ন সংজ্ঞা সীমা একটি ফাংশন এ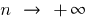

সংজ্ঞা: একটি সংখ্যা 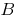বলা হয়, সীমা একটি ক্রম 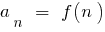জন্য যদি কোন 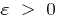নেই, যেমন সংখ্যা 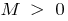যে সব জন্য 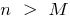নিম্নলিখিত বৈষম্য সন্তুষ্ট হয় 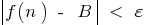অর্থাৎ

যদি ,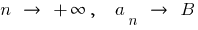

তুলনামূলক সূচক বৃদ্ধি, সূচকীয় এবং লগারিদমিক ফাংশন

• যখন

,

যে

তাহলে , যখন 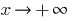একটি ফাংশন 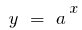বৃদ্ধি তুলনায় দ্রুততর কোন সূচকীয় ফাংশন 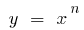যেখানে একটি প্রাকৃতিক সংখ্যা

Graphically, এই বিবৃতি, এর মানে হল যে জন্য বড় বেশি মান গ্রাফ ফাংশন 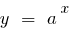(যেখানে 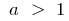) উপরে গ্রাফ এর একটি ফাংশন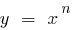

• যখন

,

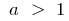
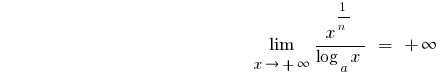যে

,

At large ;

,

তাই

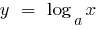যদি ফাংশন বৃদ্ধি তুলনায় ধীর ফাংশন 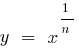(এবং বিশেষ করে, ধীর চেয়ে একটি ফাংশন 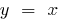বা একটি ফাংশন )

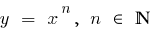Graphically, এই বিবৃতি, এর মানে হল যে জন্য বড় বেশি মান গ্রাফ ফাংশন 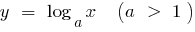মিথ্যা নীচের গ্রাফ এর একটি ফাংশন 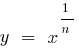(এবং বিশেষ করে নীচের গ্রাফ ফাংশন )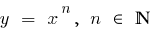