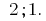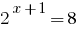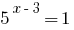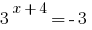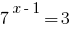সূচকীয় সমীকরণ

সমর্থন তথ্য

কোন বৃদ্ধি (কমে) ফাংশন মধ্যে প্রতিটি acquires তার মান শুধুমাত্র এক বিন্দু এই সময়ের.

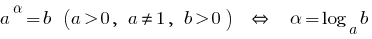
যখন 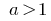সূচকীয় ফাংশন বৃদ্ধি করা হয়.

যখন ~0 সূচকীয় ফাংশন আসে.

যখন 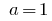সূচকীয় ফাংশন ছিল.

সিদ্ধান্ত মডেল সমীকরণ এক জানা আবশ্যক বৈশিষ্ট্য , এর শিকড় এবং ডিগ্রী.

উদাহরণ সমাধান সহজ সূচকীয় সমীকরণ

 

 

সমাধান:

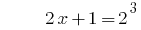
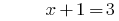
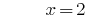
উত্তর:

 

সমাধান:

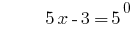
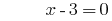
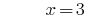
উত্তর: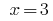

 

সমাধান:

কোন শিকড় (তাই )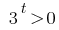

উত্তর: কোন শিকড়

 

সমাধান:

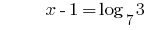
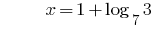
উত্তর: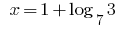

1. 
2. 
3. 
4. 

উদাহরণ সমাধান মডেল সমীকরণ দ্বারা হ্রাস করা সহজ

______________________________________________________________________

যদি বাম এবং ডান অংশ সমীকরণ হয় অর্থবোধক শুধুমাত্র কাজ, ভগ্নাংশ, শিকড় আও পরিমাণে, এটা যুক্তিযুক্ত মৌলিক সূত্র ব্যবহার করে চেষ্টা করতে রেকর্ড উভয় অংশের সমীকরণ হিসাবে ক্ষমতা এক বেস.

______________________________________________________________________

উদাহরণ 1:

Rozwarte সমীকরণ .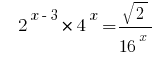

সমাধান:

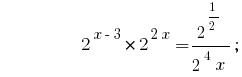
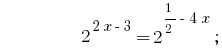
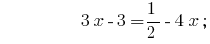
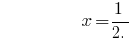
উত্তর: .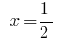

 

______________________________________________________________________

যদি এক অংশ সূচকীয় সমীকরণ একটি সংখ্যা, এবং অন্যান্য ধারণকারী সব সদস্যদের অভিব্যক্তি 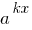(বহিঃপ্রকাশ পৃথক দ্বারা শুধুমাত্র বিনামূল্যে সদস্য), এটি সুবিধাজনক এই অংশ সমীকরণের একপাশে সরিয়ে রাখা ক্ষুদ্রতম ডিগ্রী .

______________________________________________________________________

উদাহরণ 2:

Rozwarte সমীকরণ .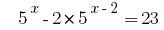

সমাধান:

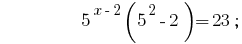
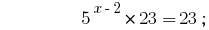
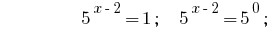
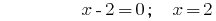
উত্তর: .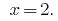

উদাহরণ আরো জটিল সূচকীয় সমীকরণ

______________________________________________________________________

পরিত্রাণ পেতে সাংখ্যিক পদ মধ্যে সূচক ব্যবহার করে (ডান-থেকে-বাম মৌলিক বৈশিষ্ট্য ডিগ্রী).

যদি সম্ভব কমাতে সব ডিগ্রী থেকে এক ভিত্তিতে এবং সঞ্চালন একটি পরিবর্তন ভেরিয়েবল.

______________________________________________________________________

উদাহরণ 3:

Rozwarte সমীকরণ .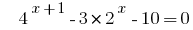

সমাধান:

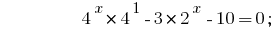
প্রদত্ত যে 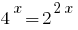, আমরা কমাতে ডিগ্রী দ্বারা একটি বেস 2: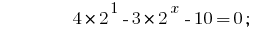

প্রতিকল্পন 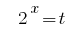দেয় সমীকরণ:

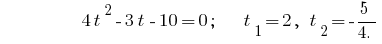
অনগ্রসর প্রতিকল্পন দেয় সমীকরণ 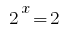, যেখানে বা 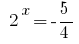- কোন শিকড়.

উত্তর: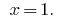

 

 

______________________________________________________________________

না হলে ডিগ্রী কমে যেতে পারে এক ভিত্তিতে হ্রাস করে চেষ্টা করুন সব ডিগ্রী থেকে দুই ঘাঁটি প্রাপ্ত, তাই হিসাবে একটি সজাতি সমীকরণ.

______________________________________________________________________

উদাহরণ 4:

Rozwarte সমীকরণ .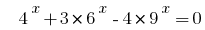

সমাধান:

দিতে যাক সব কিছুদূর দুটি ঘাঁটি 2 ও 3:

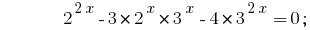
আছে একটি সজাতি সমীকরণ. তার জন্য সমাধান বিভক্ত উভয় পক্ষের দ্বারা ;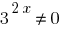

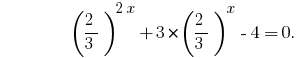
প্রতিকল্পন 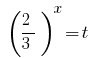দেয় সমীকরণ:

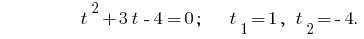
অনগ্রসর প্রতিকল্পন দেয় সমীকরণ 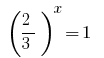, যেখানে 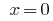বা 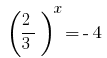- কোন শিকড়.

উত্তর: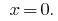

 

______________________________________________________________________

অন্যান্য ক্ষেত্রে, আমরা স্থানান্তর সব পদ সমীকরণ মধ্যে এক অংশ করার চেষ্টা করুন, এবং পচা প্রাপ্ত প্রকাশের মধ্যে কারণের বা বিশেষ কৌশল প্রয়োগ করে সমাধান যা আমরা ব্যবহার বৈশিষ্ট্য, সংশ্লিষ্ট ফাংশন.

______________________________________________________________________

উদাহরণ 5:

Rozwarte সমীকরণ .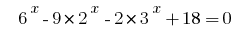

সমাধান:

যদি জোড়া করতে দলের সদস্যদের মধ্যে বাম দিকে, সমীকরণ, এবং প্রতিটি জোড়া স্ট্যান্ড আউট একটি সাধারণ ফ্যাক্টর, আমরা পেতে :

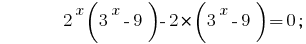
করতে বন্ধনী একটি সাধারণ ফ্যাক্টর :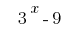

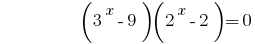
তারপর 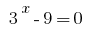বা .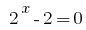

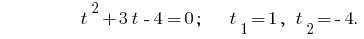
আমরা দুটি সমীকরণ 1)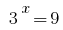যেখানে 2)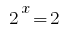 যেখানে .

উত্তর: