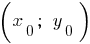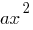সংজ্ঞা: একটি দ্বিঘাত ফাংশন বলা হয়, এর একটি ফাংশন, ফর্ম 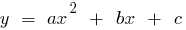 যেখানে
যেখানে 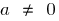
বৈশিষ্ট্য দ্বিঘাত ফাংশন
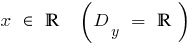
যখন 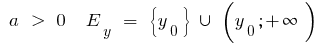
যখন 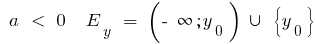
যদি 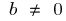 ফাংশন হয় না, এমনকি বা বিজোড়
ফাংশন হয় না, এমনকি বা বিজোড়
এ 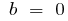 — steamroom
— steamroom
একটি দ্বিঘাত ফাংশন, ক্রমাগত এবং diferencian সমগ্র নম্বর লাইন 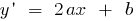
যদি 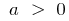 হয় হ্রাস উপর
হয় হ্রাস উপর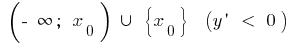 এবং ক্রমবর্ধমান উপর
এবং ক্রমবর্ধমান উপর 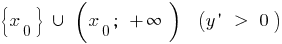 ,
, 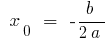 — সর্বনিম্ন
— সর্বনিম্ন 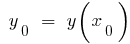 — কম
— কম
যখন 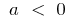 বৃদ্ধি উপর
বৃদ্ধি উপর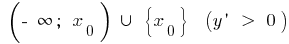 এবং হ্রাস উপর
এবং হ্রাস উপর 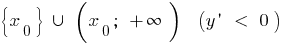 ,
, 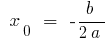 উচ্চ,
উচ্চ, 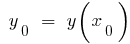 উচ্চ
উচ্চ
স্থানাঙ্ক শীর্ষবিন্দু এর অধিবৃত্ত:
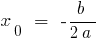 ;
; 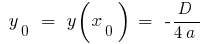 যেখানে
যেখানে 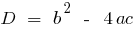
The axis of symmetry এর একটি প্যারাবোলা 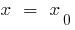
- সুযোগ

- একাধিক মান

- প্যারিটি বিজোড় প্যারিটি
- ধারাবাহিকতা এবং differentiability
- বৃদ্ধি এবং হ্রাস, extrema
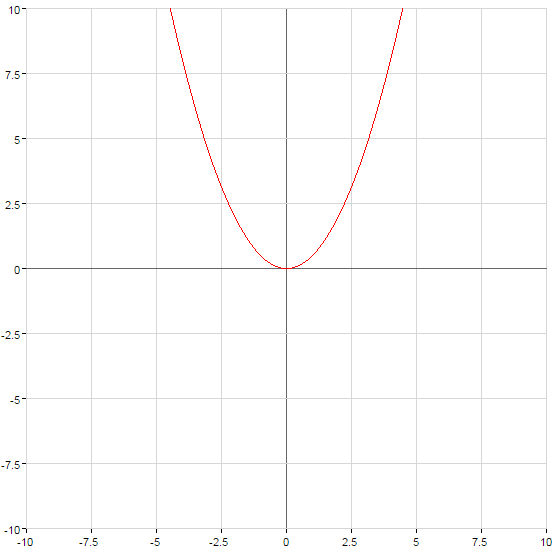
- এর গ্রাফ একটি দ্বিঘাত ফাংশন সবসময় একটি পরাবৃত্তযার শাখা পরিচালিত হয় যখন ঊর্ধ্বে
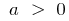 এবং নিচে যখন
এবং নিচে যখন 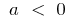
গ্রাফ এর দ্বিঘাত ফাংশন

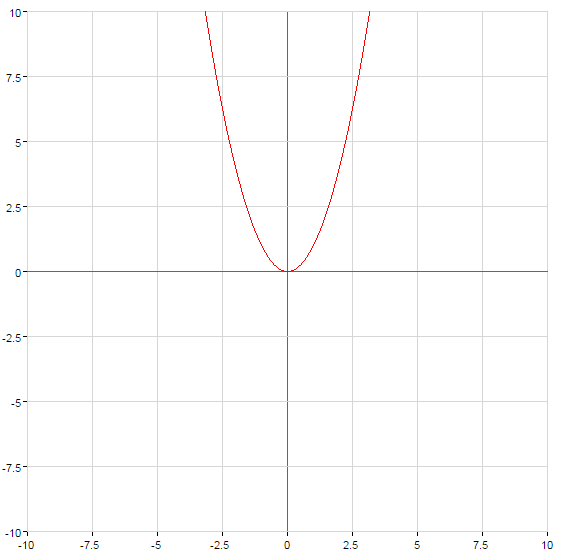

প্রতিসাম্য অক্ষ আপেক্ষিক 
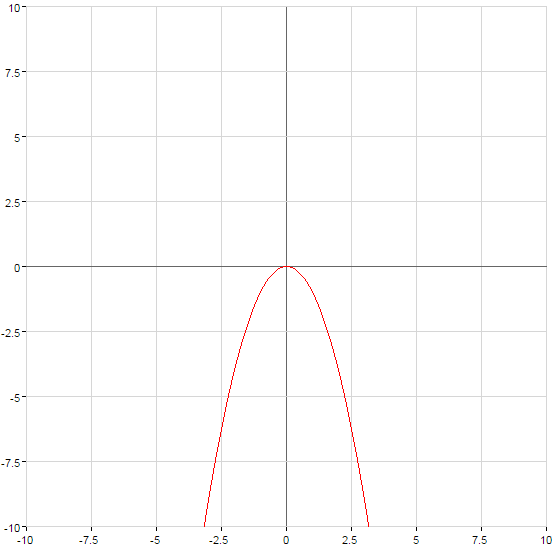

গ্রাফ ফাংশন প্রসারিত হয় 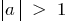 বা প্রসারিত
বা প্রসারিত  দ্বারা ইউনিট সংখ্যা সমান নম্বর এবং
দ্বারা ইউনিট সংখ্যা সমান নম্বর এবং
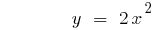
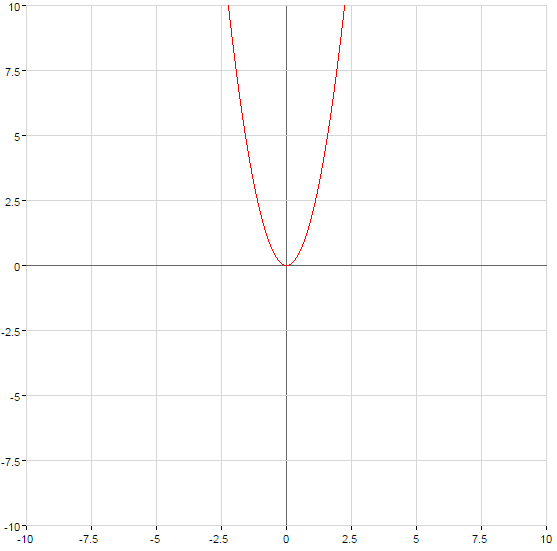
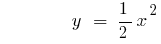
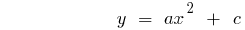
গ্রাফ ফাংশন রি এ 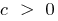 বা বৃক্ষের পতন হয় যখন
বা বৃক্ষের পতন হয় যখন 
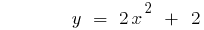
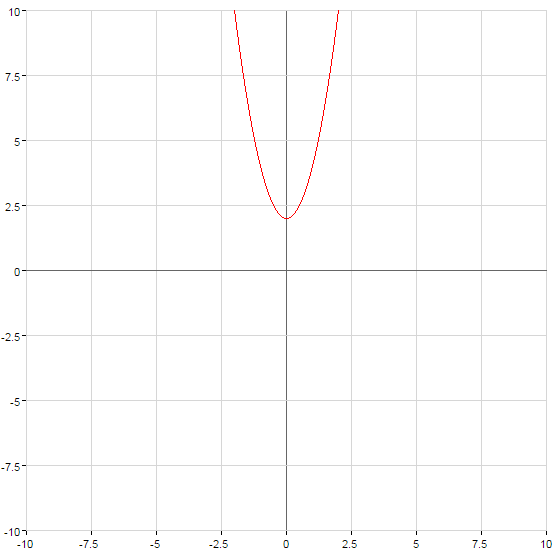
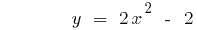
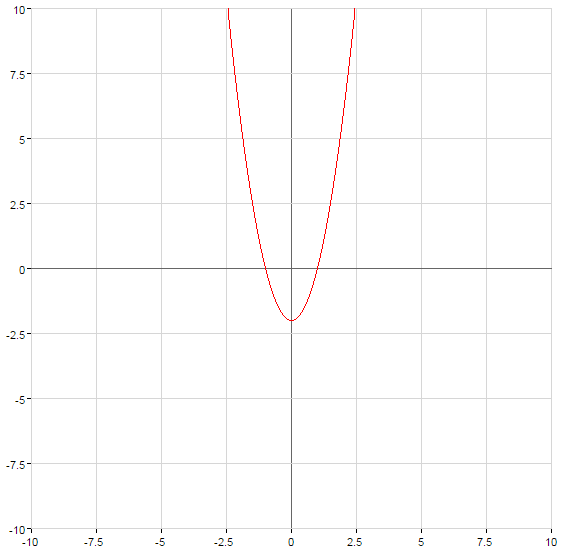
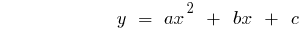
এই অধিবৃত্ত ক্রস অক্ষ  সময়ে বৃষ্টিপাতের
সময়ে বৃষ্টিপাতের
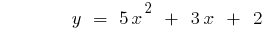
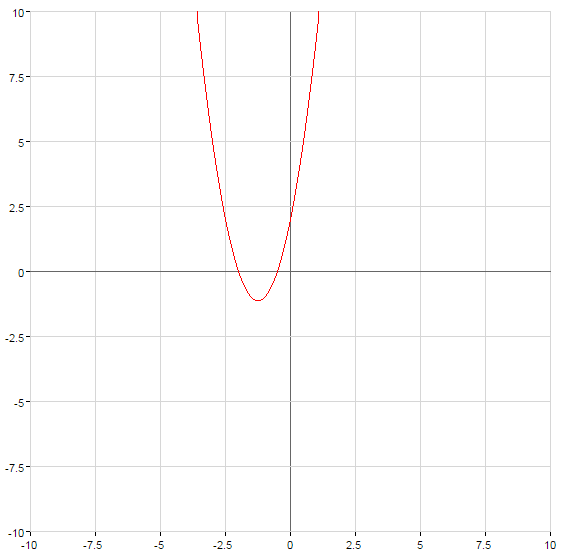
কিভাবে গ্রাফ দ্বিঘাত ফাংশন
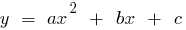
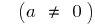
এবং পদ্ধতি
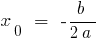
যখন 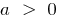 শাখা আপ সঙ্গে,
শাখা আপ সঙ্গে, 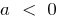 শাখা নিচে
শাখা নিচে
- নিরূপণ করতে ভুজ সমাজের সারাংশ
- বিকল্প
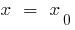 মধ্যে সমীকরণ এবং নিরূপণ y coordinate of the top —
মধ্যে সমীকরণ এবং নিরূপণ y coordinate of the top — 
- To build a sketch of the অধিবৃত্ত (
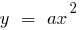 ) শীর্ষবিন্দু সময়ে
) শীর্ষবিন্দু সময়ে 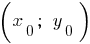
দ্বিতীয় পদ্ধতি
(ধরে অক্ষের  উপর
উপর 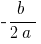 , অক্ষের
, অক্ষের 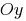 উপর
উপর 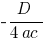 )
)
- Razvesti দ্বিঘাত সমীকরণ
- ব্যবহার করে প্রাথমিক রূপান্তরের গ্রাফ, সম্পাদন করার জন্য একটা সমান্তরাল স্থানান্তর একটি প্যারাবোলা
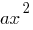




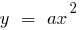 ) শীর্ষবিন্দু সময়ে
) শীর্ষবিন্দু সময়ে