ধারণা বিপরীত ফাংশন: যাক ফাংশন  লাগে প্রতি মূল্য একটি একক বিন্দু মধ্যে তার ডোমেইন (যেমন একটি ফাংশন বলা হয়, invertible ). তারপর প্রতিটি সংখ্যার জন্য
লাগে প্রতি মূল্য একটি একক বিন্দু মধ্যে তার ডোমেইন (যেমন একটি ফাংশন বলা হয়, invertible ). তারপর প্রতিটি সংখ্যার জন্য  ( থেকে ফাংশন সেট মান
( থেকে ফাংশন সেট মান  ) নেই, একটি একক মূল্য
) নেই, একটি একক মূল্য  ( ব্যাপ্তি ফাংশন
( ব্যাপ্তি ফাংশন  ) যেমন যে
) যেমন যে 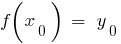 . বিবেচনা ফাংশন
. বিবেচনা ফাংশন 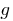 যে প্রতিটি সংখ্যা
যে প্রতিটি সংখ্যা  রাখা, সংখ্যা
রাখা, সংখ্যা  , যে হয়
, যে হয় 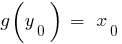 . এই ক্ষেত্রে, ফাংশন
. এই ক্ষেত্রে, ফাংশন 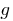 বলা হয়, বিপরীত ফাংশন
বলা হয়, বিপরীত ফাংশন  .
.
বৈশিষ্ট্য বিপরীত ফাংশন
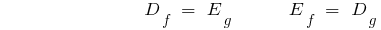
- সুযোগ, সরাসরি ফাংশন, সেট মান, বিপরীত, এবং সেট মান, সরাসরি ফাংশন, সুযোগ ফিরে.
- যদি ফাংশন বৃদ্ধি করা হয় (হ্রাস) উপর কিছু ব্যবধান, তারপর, এটা একটি বিপরীত ফাংশন উপর এই ব্যবধান বৃদ্ধি পায়, যা যদি সরাসরি ফাংশন বৃদ্ধি এবং হ্রাস, যদি ভিডিও বৈশিষ্ট্য মধ্যে আসে.
- গ্রাফ সরাসরি এবং বিপরীত ফাংশন আছে, প্রতিসম থেকে সম্মান সঙ্গে, লাইন
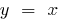 (দ্বিখণ্ডক প্রথম এবং তৃতীয় তুল্য কোণ)
(দ্বিখণ্ডক প্রথম এবং তৃতীয় তুল্য কোণ)
উদাহরণ বিপরীত ফাংশন
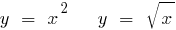
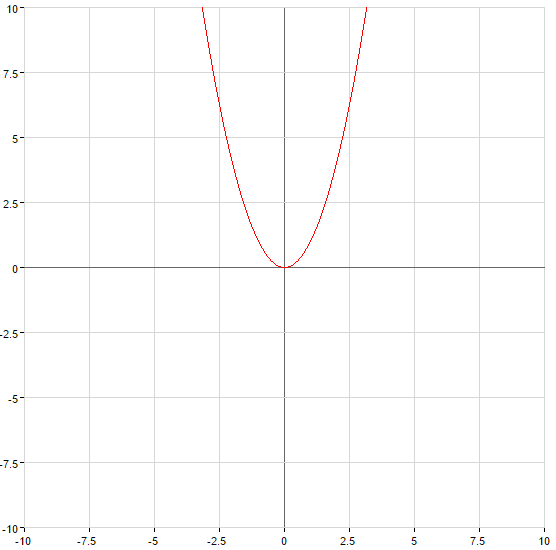
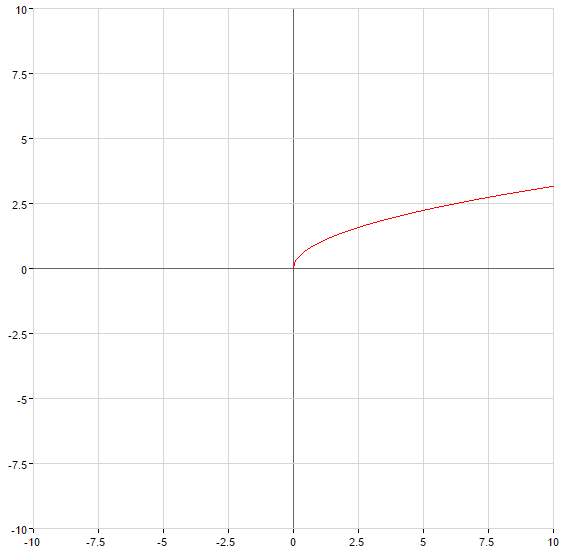
একটি উদাহরণ খোঁজার বিপরীত ফাংশন
উদাহরণ: to Find the বিপরীত ফাংশন জন্য ফাংশন: 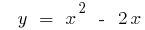
সমাধান: এটি যেখানে প্রদত্ত ফাংশন বৃদ্ধি এবং হ্রাস 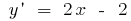 . তারপর
. তারপর 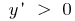 যখন
যখন 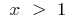 একটি ফাংশন বৃদ্ধি করা হয়
একটি ফাংশন বৃদ্ধি করা হয় 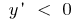 যখন
যখন 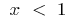 ফাংশন কমে যায়.
ফাংশন কমে যায়.
প্রতিটি সময়ে এই অন্তর 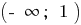 ও
ও 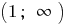 লেখার সূত্র এর বিপরীত ফাংশন. যেহেতু,
লেখার সূত্র এর বিপরীত ফাংশন. যেহেতু, 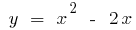 তারপর
তারপর 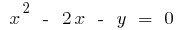 .
.
অত: পর 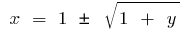 , যে হয়, যখন
, যে হয়, যখন 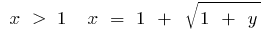 , এবং যখন
, এবং যখন 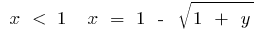 . পরিবর্তন, প্রতীক, প্রথাগত, আমরা পেতে: জন্য একটি ফাংশন
. পরিবর্তন, প্রতীক, প্রথাগত, আমরা পেতে: জন্য একটি ফাংশন 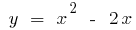 সঙ্গে,
সঙ্গে, 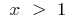 বিপরীত, একটি ফাংশন
বিপরীত, একটি ফাংশন 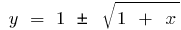 যখন
যখন 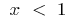 বিপরীত ফাংশন একটি ফাংশন
বিপরীত ফাংশন একটি ফাংশন 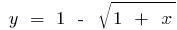 .
.

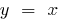 (দ্বিখণ্ডক প্রথম এবং তৃতীয় তুল্য কোণ)
(দ্বিখণ্ডক প্রথম এবং তৃতীয় তুল্য কোণ)