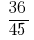ব্যবহার করে মৌলিক বৈশিষ্ট্য ভগ্নাংশ , এটা সম্ভব প্রতিস্থাপন করতে, একটি নির্দিষ্ট ভগ্নাংশ অন্যদের এই সমান, কিন্তু সঙ্গে একটি ছোট লব ও হর. এই প্রতিকল্পন বলা হয়, হ্রাস ভগ্নাংশ.
কমাতে একটি ভগ্নাংশ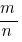 
আপনি খুঁজে বের করতে হবে সর্বশ্রেষ্ঠ সাধারণ গুণনীয়ক আছে , তার লব ও হর: GCD (m,n), এবং তারপর বিভক্ত লব ও হর দ্বারা এই সংখ্যা. যদি GCD (m,n)=1, ভগ্নাংশ হতে পারে না কমান.
উদাহরণ হ্রাস ভগ্নাংশ
উদাহরণ 1: প্রক্রিয়া সহজ ভগ্নাংশ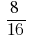 
সমাধান: GCD (8;16) = 8, তারপর
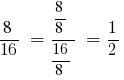
উদাহরণ 2: ভগ্নাংশ অজটিল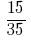 
সমাধান: GCD (5;35) = 5, তারপর
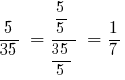
উদাহরণ 3: ভগ্নাংশ অজটিল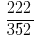 
সমাধান: GCD (222;352) = 2 তাহলে, তারপর
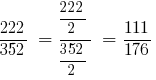
উদাহরণ 4: প্রক্রিয়া সহজ ভগ্নাংশ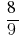 
সমাধান: GCD (8;9) = 1, তাহলে, সংজ্ঞা দ্বারা, ভগ্নাংশ হতে পারে না কমান.
এর নির্মাণ ভগ্নাংশ জন্য একটি সাধারণ হর
ভগ্নাংশ হ্রাস করার জন্য সর্বনিম্ন সাধারণ হর. এটা সমান, অন্তত সাধারণ গুণিতক (LCM) হর, এই ভগ্নাংশ যে, ক্ষুদ্রতম যে সংখ্যা দ্বারা বিভাজ্য হয় হর প্রথম এবং দ্বিতীয় ভগ্নাংশ.
এর নির্মাণ ভগ্নাংশ উদাহরণ
উদাহরণ 1: আনতে সাধারণ হর: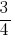 
এবং
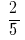
NSK (4, 5) = 20.
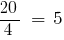— অক্জিলিয়ারী গুণক প্রথম ভগ্নাংশ
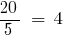— অক্জিলিয়ারী গুণক জন্য দ্বিতীয় ভগ্নাংশ.
তারপর:
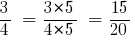
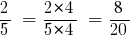
উত্তর: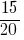 
এবং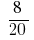 
উদাহরণ 2: কমাতে একটি সাধারণ হর: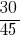 
এবং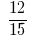
NSK (45, 15) = 45.
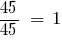— অক্জিলিয়ারী গুণক প্রথম ভগ্নাংশ
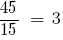— অক্জিলিয়ারী গুণক জন্য দ্বিতীয় ভগ্নাংশ.
তারপর:
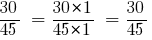
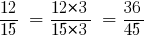
উত্তর: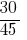 
এবং