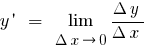
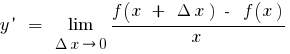
সংজ্ঞা: ডেরিভেটিভ ফাংশন 
সময়ে 
বলা হয়, সীমা অনুপাত বৃদ্ধি, ফাংশন এ বিন্দু থেকে, বৃদ্ধি, যুক্তি যখন বৃদ্ধি যুক্তি থাকে শূন্য (বোঝান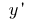 
বা 
)
অপারেশন খুঁজে বের করার একটি অমৌলিক বলা হয়, বিভেদ
ধারণা বৃদ্ধির যুক্তি এবং ফাংশন
বৃদ্ধির যুক্তি
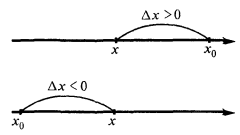
বৃদ্ধি ফাংশন
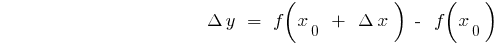
ডেরাইভেটিভস এর প্রাথমিক ফাংশন
ডেরাইভেটিভস এর প্রাথমিক ফাংশন পাওয়া যায়, ব্যবহার করে টেবিল:
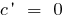
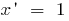
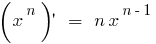
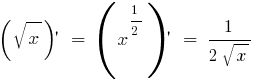
সব ডেরাইভেটিভস এর প্রাথমিক ফাংশন পাওয়া যাবে এখানে!
কম্পাইল ফাংশন. এটি কিভাবে কম্পাইল ফাংশন
ডেরিভেটিভ এর সমষ্টি (পার্থক্য) এর দুটি ফাংশন আছে, প্রতিটি যা একটি অমৌলিক সমান সমষ্টি (পার্থক্য) ডেরাইভেটিভস, এই ফাংশন:
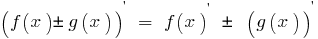
ডেরিভেটিভ কাজ করে, এর দুটি ফাংশন আছে, প্রতিটি যা একটি অমৌলিক সমান সমষ্টি পণ্য প্রতিটি ফাংশন মধ্যে ডেরিভেটিভ দ্বিতীয় ফাংশন:
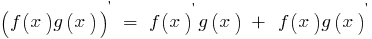
ডেরিভেটিভ শেয়ারের শেয়ারের দুটি ফাংশন f(x) এবং g(x) আছে, প্রতিটি যা ডেরিভেটিভ g(x)≠0, দ্বারা দেওয়া হয়
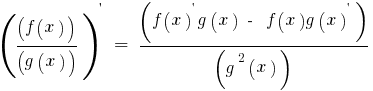
ধ্রুব ফ্যাক্টর হতে পারে থেকে সরানো চিহ্ন ডেরিভেটিভ:
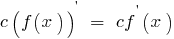
সূত্র বলা নিয়ম বিভেদ.
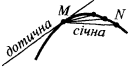
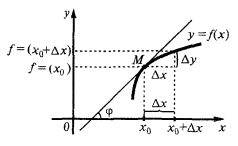
জ্যামিতিক অর্থ ডেরিভেটিভ
স্পর্শক করতে বক্ররেখা একটি নির্দিষ্ট সময়ে 
বলা হয়, সীমিত এর অবস্থান secant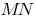 
যখন পয়েন্ট 
সমীপবর্তী হয় একটি বক্ররেখা বরাবর বিন্দু
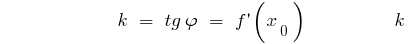— ঢাল এর স্পর্শক
সমীকরণ থেকে স্পর্শক থেকে গ্রাফ ফাংশন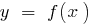 
সঙ্গে সময়ে Alsou 
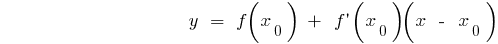
মান ডেরিভেটিভ সময়ে সমান কৌণিক সহগ, স্পর্শক থেকে গ্রাফ ফাংশন সঙ্গে সময়ে Alsou এবং সমান স্পর্শক এর কোণ বাঁক এই স্পর্শক অক্ষ থেকে 
শারীরিক অর্থ ডেরিভেটিভ
ডেরিভেটিভ বর্ণনা করে পরিবর্তনের হার এর ফাংশন পরিবর্তন যখন আপনি যুক্তি
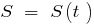— নির্ভরতা ভ্রমণ দূরত্ব, সময় থেকে
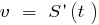— গতি rectilinear গতি
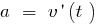— ত্বরণ গতি rectilinear