Означення: Нехай функція 
визначена на всій числовій прямій. Число 
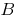називається границею функції при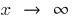 
, якщо для довільного 
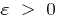знайдеться таке число 
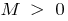, що для всіх 
, які задовільняють умову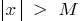 
, виконується нерівність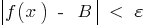 
При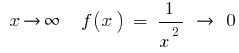 
, тобто при великих (за модулем) значеннях число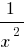 
дуже мало відрізняється від числа 0
Якщо поведінка функції різна при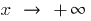 
та при 
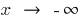, то окремо розглядають 
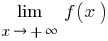(в означенні беруть 
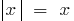) і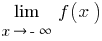 
(в означенні беруть 
)
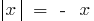Границя послідовності
Оскільки послідовність є функцією натурального аргументу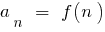 
, то означення границі послідовності при 
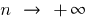цілком збігається з означенням границі функції при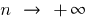
Означення: Число 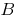називається границею послідовності 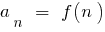, якщо для довільного 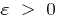існує таке число 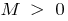, що для всіх 
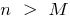, виконується нерівність 
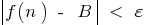тобто
Якщо при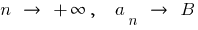 
, то
Порівняння росту показникової, степеневої та логарифмічної функцій
- При
,
тобто
Якщо 
, то при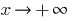 
функція 
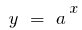зростає швидше від будь-якої степеневої функції 
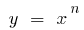, де 
— натуральне число
Графічно це твердження означає, що при досить великих значеннях графік функції 
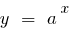(де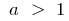 
) розташовано вище від графіка функції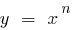 
- При
,
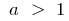
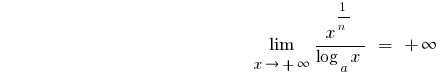тобто
,
При великих ;
,
тому
Якщо , то функція 
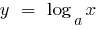зростає повільніше, ніж функція 
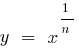(і тим більш повільніше, ніж функція 
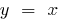або функція 
)
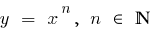Графічно це твердження означає, що при досить великих значеннях графік функції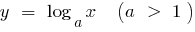 
розташовано нижче від графіка функції 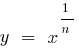(і тим більш нижче від графіків функцій )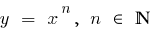