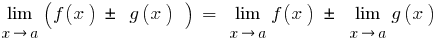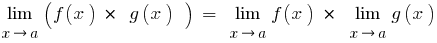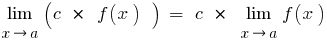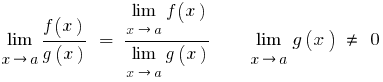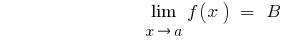
Де  — число або один із символів
— число або один із символів 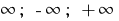
Означення: Число 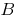 називається границею функції
називається границею функції  в точці
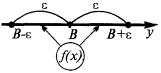
в точці  (при
(при  , що прямує до
, що прямує до  ), якщо для будь-якого додатного
), якщо для будь-якого додатного 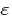 знайдеться таке додатне число
знайдеться таке додатне число 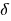 , що при всіх
, що при всіх 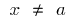 , які задовільняють нерівність
, які задовільняють нерівність 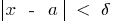 , виконується нерівність
, виконується нерівність 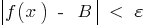
Математичний запис виразів 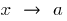 та
та 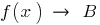
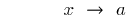
Точка  знаходиться від точки
знаходиться від точки  на малій відстані (менше
на малій відстані (менше 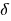 )
) 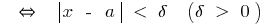
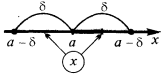
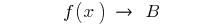
Значення  на числовій прямій знаходиться на малій відстані від
на числовій прямій знаходиться на малій відстані від 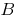 (менше
(менше 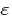 )
) 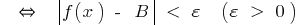
Властивості границі функції
Якщо функція  має границю при
має границю при 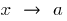 , то границя — єдина
, то границя — єдина
Границя сталої функції дорівнює цій самій сталій
Границя неперевної функції при 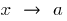 дорівнює значенню функції в точці
дорівнює значенню функції в точці 
- Якщо
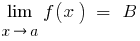 , то
, то 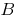 — єдине
— єдине 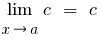 , де
, де 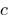 — стала
— стала — неперервна в точці
— неперервна в точці  функція
функція 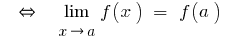 (за означенням неперервної функції
(за означенням неперервної функції
Теореми про границі
Перша визначна границя
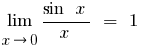
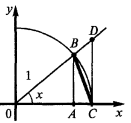

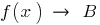
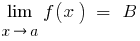 , то
, то 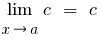 , де
, де 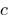 — стала
— стала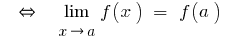 (за означенням
(за означенням