تعريف: معادلة مع متغير واحد  هو المساواة مع متغير واحد
هو المساواة مع متغير واحد  ، في العام الذي شكل كتب مثل هذا:
، في العام الذي شكل كتب مثل هذا: 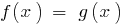
تعريف: جذر (أو rozvyazka) المعادلة  يسمى قيمة المتغير الذي يجعل المعادلة الحقيقية العددية المساواة.
يسمى قيمة المتغير الذي يجعل المعادلة الحقيقية العددية المساواة.
Razvesti المعادلة يعني إيجاد جميع جذوره (تقاطعات) أو أن تظهر أنها ليست كذلك.
مجال القيم المسموح بها (odz) المعادلة
تعريف: مجال القيم المسموح بها (مجموعة التعريف) من المعادلة — النطاق العام على وظائف 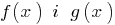 دائمة في اليسار واليمين أجزاء من المعادلة.
دائمة في اليسار واليمين أجزاء من المعادلة.
العثور على مجال القيم المسموح بها (odz)
على سبيل المثال
مجموعة المعادلة: 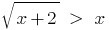
درهم: 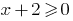 أي
أي 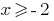 ، مجال الوظيفة
، مجال الوظيفة 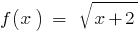 يتم تحديدها من قبل الشرط
يتم تحديدها من قبل الشرط 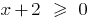 ، مجال الوظيفة
، مجال الوظيفة 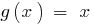 هي مجموعة من الأعداد الحقيقية.
هي مجموعة من الأعداد الحقيقية.
المعادلات التحقيق
إن كل جذر المعادلة الأولى هو جذر المعادلة الثانية الثانية المعادلة يسمى نتيجة المعادلة الأولى.
إذا صلاحية أول المساواة يعني صحة كل مما يلي ، ثم ، adejumo المعادلة هو نتيجة
لذلك ، عند استخدام المعادلات تأثير التحقق من الجذور عن طريق الإنابة في المعادلة الأصلية هو جزء من الحل.
مثال 1
Razvesti المعادلة: 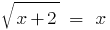
الحل:
دعونا نبني كل أجزاء المعادلة في مربع:
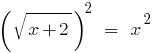 ;
;
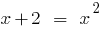 ;
;
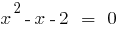 ;
;
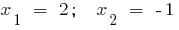 .
.
هل فحص الخلفية. 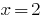 — الجذر
— الجذر 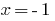 هو خارج الجذر.
هو خارج الجذر.
الجواب: 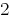 .
.
أي ما يعادل المعادلات
تعريف: ما يعادل (ما يعادل) المعادلات — اثنين من المعادلات التي للعديد من درهم لديهم نفس النتيجة ، أي أن كل حل المعادلة الأولى هي rozvyazka الثاني ، والعكس بالعكس.
بعض النظريات حول على قدم المساواة السائد إما المعادلات
نظرية 1: إذا كان جزء واحد من المعادلة للانتقال إلى جزء آخر من الشروط مع علامة المقابلة ، نحصل على معادلة أي ما يعادل معين (أي مجموعة).
نظرية 2: إذا كان كل من أجزاء من المعادلة تكون مضروبة أو مقسوما على نفس الرقم لا يساوي الصفر (أو نفس وظيفة محددة لا يساوي صفر على معرفات من المعادلة المعطاة) ، نحصل على المعادلة أي ما يعادل واحد معين.
نظرية 3: إذا كان كل من أجزاء من المعادلة 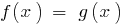 أن تأخذ في الارتفاع (أو تنازلي) وظيفة
أن تأخذ في الارتفاع (أو تنازلي) وظيفة 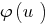 وليس vdbase تضييق معرفات من المعادلة المعطاة
وليس vdbase تضييق معرفات من المعادلة المعطاة 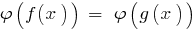 سوف يكون معادلا معين ( DHS).
سوف يكون معادلا معين ( DHS).
نتائجها الطبيعية من النظريات حول على قدم المساواة السائد إما المعادلات
النتيجة: لأن وظيفة 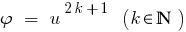 زيادة مفردة النغمة ، ثم
زيادة مفردة النغمة ، ثم
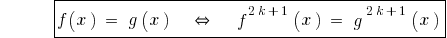 .
.
في عرض كل جزء من المعادلة في الغريب الطبيعية درجة المعادلة الناتجة عن ذلك يعادل هذا.
النتيجة: لأن وظيفة 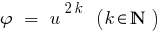 زيادة مفردة النغمة إلا إذا كان
زيادة مفردة النغمة إلا إذا كان 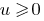 في حالة عندما يكون كلا أجزاء من المعادلة newmn ، من خلال رفع كل الأجزاء حتى إلى درجة الطبيعية المعادلة الناتجة عن ذلك يعادل هذا.
في حالة عندما يكون كلا أجزاء من المعادلة newmn ، من خلال رفع كل الأجزاء حتى إلى درجة الطبيعية المعادلة الناتجة عن ذلك يعادل هذا.
