استمرارية دالة في نقطة
تعريف: وظيفة  يسمى المستمر في
يسمى المستمر في 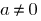 إذا
إذا 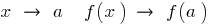 ، هذا هو
، هذا هو 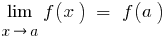 .
.
وظائف مستمرة على الفاصل الزمني
تعريف: إذا كانت الدالة  مستمرة عند كل نقطة من بعض الفاصل
مستمرة عند كل نقطة من بعض الفاصل  ، ويسمى المستمر على الفاصل الزمني
، ويسمى المستمر على الفاصل الزمني  .
.
استمرارية خصائص وظائف
مثال على استمرارية وظيفة
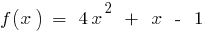 وظيفة مستمرة (متعدد الحدود)
وظيفة مستمرة (متعدد الحدود)
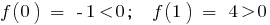 لذا على الفترة (0;1) هناك نقطة
لذا على الفترة (0;1) هناك نقطة  حيث وظيفة يساوي 0:
حيث وظيفة يساوي 0: 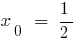
مثال على استمرارية وظيفة
مثال على استمرارية وظيفة
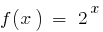 وظيفة مستمرة. إذا
وظيفة مستمرة. إذا
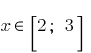 ثم
ثم 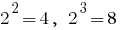 . لأن
. لأن 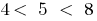 هناك نقطة
هناك نقطة  فيها
فيها 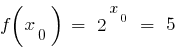 .
.
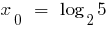
سيادة إيجاد أكبر وأصغر snakeb وظائف.
- إذا المستمر على wtrysku
 الفرد يكتسب في نهايات هذا الجزء القيم من علامات مختلفة ، ثم في مرحلة هذا الجزء انها تأخذ على قيمة صفر.
الفرد يكتسب في نهايات هذا الجزء القيم من علامات مختلفة ، ثم في مرحلة هذا الجزء انها تأخذ على قيمة صفر. - إذا على الفاصل الزمني
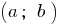 الدالة
الدالة  مستمرة و لا تتحول إلى صفر على هذا الفاصل وظيفة يبقي ثابت علامة.
مستمرة و لا تتحول إلى صفر على هذا الفاصل وظيفة يبقي ثابت علامة. - دالة
 مستمرة على فاصل زمني
مستمرة على فاصل زمني  يأخذ على كل القيم المتوسطة بين قيم هذه الوظيفة في النقاط المتطرفة ، أي بين
يأخذ على كل القيم المتوسطة بين قيم هذه الوظيفة في النقاط المتطرفة ، أي بين 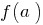 و
و 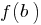 .
. - وظيفة
 المستمر على قطاع
المستمر على قطاع  يقتصر على هذا الجزء, ثم هناك وجود اثنين من أرقام
يقتصر على هذا الجزء, ثم هناك وجود اثنين من أرقام  و
و  للجميع
للجميع 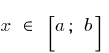 المساواة
المساواة 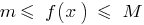 .
. - مقدار الفرق و العمل المستمر على هذا الفاصل وظيفة مستمر على نفس الفاصل وظيفة. حاصل اثنين المستمر وظائف وظيفة مستمرة في جميع النقاط التي القاسم ليس peretolchina إلى الصفر.
- عكس وظيفة مستمرة على فترة معينة ، هو مستمر على هذا الفاصل.
- إذا كانت وظيفة
 لديها المشتقة
لديها المشتقة  ، ثم هو مستمر في تلك المرحلة.
، ثم هو مستمر في تلك المرحلة.
كسر نقطة
تعريف: نقطة  نقطة فاصل وظيفة
نقطة فاصل وظيفة 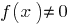 ، إذا كان الموضوع
، إذا كان الموضوع  ليس شرط أنه عندما
ليس شرط أنه عندما 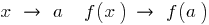 .
.
أمثلة على وظائف مع كسر نقطة
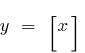 نقطة كسر كل النقاط صحيحة
نقطة كسر كل النقاط صحيحة
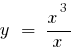 — كسر - 0
— كسر - 0
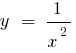 — كسر - 0
— كسر - 0

 الفرد يكتسب في نهايات هذا الجزء القيم من علامات مختلفة ، ثم في مرحلة هذا الجزء انها تأخذ على قيمة صفر.
الفرد يكتسب في نهايات هذا الجزء القيم من علامات مختلفة ، ثم في مرحلة هذا الجزء انها تأخذ على قيمة صفر.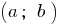 الدالة
الدالة 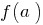 و
و 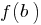 .
. و
و  للجميع
للجميع 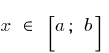 المساواة
المساواة 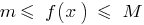 .
.