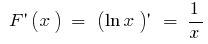Inicial
Definición: la Función 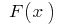 se llama inicial para la función
se llama inicial para la función  en el intervalo, si para cualesquiera
en el intervalo, si para cualesquiera  de este espacio
de este espacio 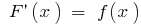
Ejemplos
- Para la función
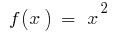 en el intervalo
en el intervalo 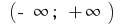 inicial es
inicial es 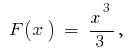 debido a que
debido a que 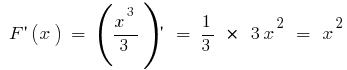
- Para la función
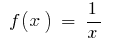 en el intervalo
en el intervalo 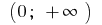 inicial es
inicial es 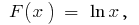 debido a que
debido a que 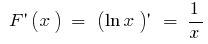
La principal propiedad de первообразных
Si la función 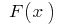 es original para la función
es original para la función  en el intervalo dado, y
en el intervalo dado, y 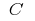 es una constante, entonces la función
es una constante, entonces la función 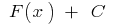 es también la inicial de la función
es también la inicial de la función 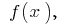 cuando este toda первообразная para la función
cuando este toda первообразная para la función  en el intervalo puede ser escrita en la forma
en el intervalo puede ser escrita en la forma 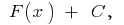 donde
donde 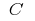 es arbitraria fue
es arbitraria fue
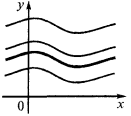
El significado geométrico
Gráficos de cualquier первообразных esta función se obtienen entre sí en paralelo a lo largo del eje 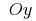
La integral indefinida
Definición:Conjunto de todas las первообразных esta función  se llama incierta integrada y se indica mediante el símbolo
se llama incierta integrada y se indica mediante el símbolo 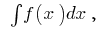 es decir,
es decir, 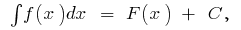 donde
donde 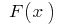 es uno de первообразных funciones
es uno de первообразных funciones 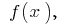 y
y 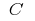 cierto fue
cierto fue
Reglas de integración
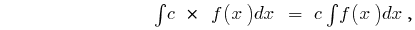 donde
donde 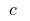 se convirtió en la
se convirtió en la
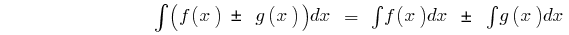
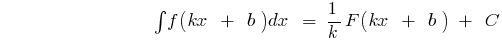

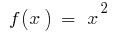 en el intervalo
en el intervalo 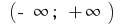 inicial es
inicial es 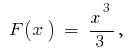 debido a que
debido a que 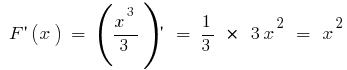
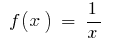 en el intervalo
en el intervalo 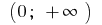 inicial es
inicial es 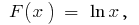 debido a que
debido a que