Definición: Показниково-степенное la ecuación  es una ecuación que contiene las expresiones de tipo
es una ecuación que contiene las expresiones de tipo 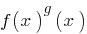 , es decir, una ecuación de la forma
, es decir, una ecuación de la forma 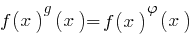
Los principales métodos de decisión показниково-степенных ecuaciones y desigualdades
 Para el caso de f(x)>0
Para el caso de f(x)>0
Ejemplo 1
Soluciones:
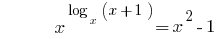
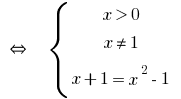
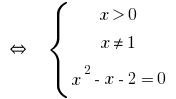
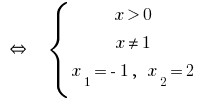
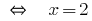
Respuesta: 
Ejemplo 2
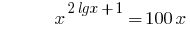
Soluciones:
En las eds  de ambas partes de la ecuación son positivos, por lo tanto, después de логарифмирования en base 10, obtenemos la ecuación que constituyen el
de ambas partes de la ecuación son positivos, por lo tanto, después de логарифмирования en base 10, obtenemos la ecuación que constituyen el 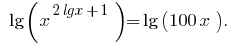
De aquí 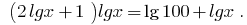
Sustitución de la 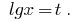
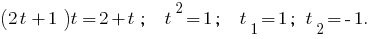
Entonces 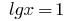 o
o 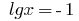 , es decir,
, es decir, 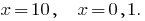 (ambos de la raíz llevan a la eds)
(ambos de la raíz llevan a la eds)
Respuesta: 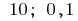
 Para el caso de f(x) — arbitraria de la expresión
Para el caso de f(x) — arbitraria de la expresión
Ejemplo 3
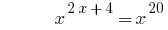
Soluciones:
Si se considera la base de  un número,
un número,
1) si 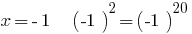 es correcta la igualdad;
es correcta la igualdad;
2) cuando 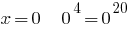 correctamente;
correctamente;
3) cuando 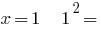 correctamente;
correctamente;
4) 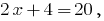 es decir, la
es decir, la 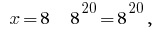 verdadera igualdad.
verdadera igualdad.
Respuesta: 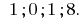
Nota: Si considerar la base de la  variable, entonces la función
variable, entonces la función 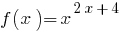 se considera que ha surgido sólo cuando
se considera que ha surgido sólo cuando 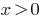 . Desde este punto de vista, esta ecuación sólo tiene dos raíces:
. Desde este punto de vista, esta ecuación sólo tiene dos raíces: 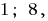

 Para el caso de f(x)>0
Para el caso de f(x)>0