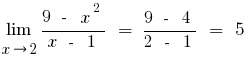
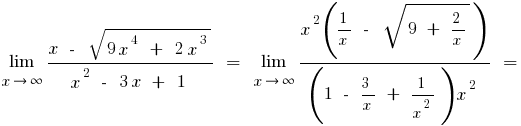
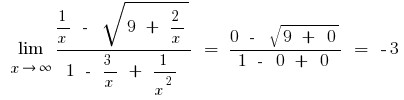
a) intentando descomponer el numerador y el pronombre en el multiplicador
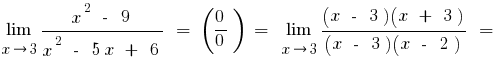
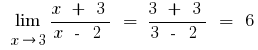
b) si el numerador o el denominador incluye la expresión con la cuadrada o cúbica de la raíz, se multiplica el numerador y el denominador de expresiones correspondientes para deshacerse de las raíces (a veces introducen la sustitución y la expresión con la raíz representan una nueva variable)
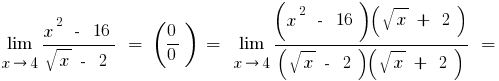
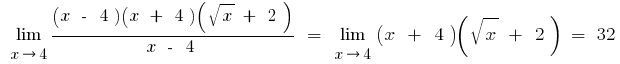
a) si bajo el signo de límite están trigonométricas o funciones trigonométricas inversas, los límites que reducen la primera sobresaliente de la frontera

o sus variaciones



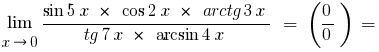
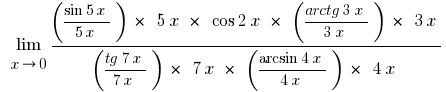
Reduciendo el numerador y el denominador en las variables, detrás de los paréntesis, teniendo en cuenta que 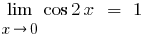 , y teniendo en cuenta перщу destacado de la frontera y sus variaciones, obtenemos
, y teniendo en cuenta перщу destacado de la frontera y sus variaciones, obtenemos 
- Aprovechando la continuidad de la función
 , intentando sustituir los valores
, intentando sustituir los valores  en la función de
en la función de 
- Si se calcula el límite cuando
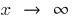 , intentando en el numerador y местоимении soportar fuera de los corchetes el más alto grado de desconocido
, intentando en el numerador y местоимении soportar fuera de los corchetes el más alto grado de desconocido - Si como resultado de la búsqueda
 recibieron una expresión del tipo
recibieron una expresión del tipo 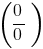 ,
,

 , intentando sustituir los valores
, intentando sustituir los valores  en la función de
en la función de 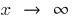 , intentando en el numerador y местоимении soportar fuera de los corchetes el más alto grado de desconocido
, intentando en el numerador y местоимении soportar fuera de los corchetes el más alto grado de desconocido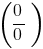 ,
,