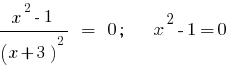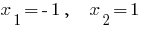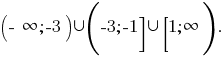La decisión de las desigualdades mediante representaron transformaciones
- La conversión de asegurar la conservación correcta de la igualdad
- Comprobación de las raíces de la sustitución en el origen de la desigualdad
Solución de ecuaciones mediante el método de los intervalos de
- Encontrar eds.
- Encontrar los ceros de la función:

- Señalar los ceros en las eds y encontrar el signo de la función f(x) en cada intervalo, en que se divide la eds.
- Escribir la respuesta, teniendo en cuenta el carácter teórico de la desigualdad.
La decisión de las desigualdades. El método de los intervalos.
- Encontrar eds.
- Encontrar los ceros de la función:

- Señalar los ceros en las eds y encontrar el signo de la función f(x) en cada intervalo, en que se divide la eds.
- Escribir la respuesta, teniendo en cuenta el carácter teórico de la desigualdad.
Ejemplo 1.
Розвяжіть la desigualdad: 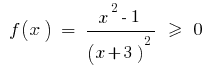
Розвязання. Que 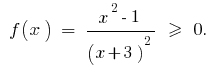
- Eds:
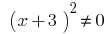 por tanto
por tanto 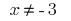 .
. - Los ceros de la función:

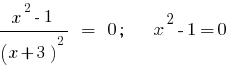
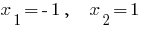
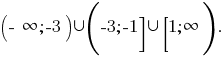
Ejemplo 2.
Especificar el menor número entero que es розвязком irregularidades
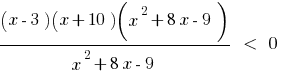
Розвязання. Permitir que la desigualdad según el método de intervalos.
Eds: 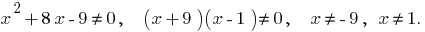
Encontraremos los ceros de la función: 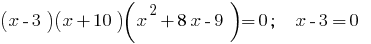 o
o 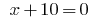
Entonces 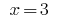 o
o 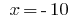 .
.
Representan los ceros y las eds y encontramos el signo de la función en cada intervalo.
Entonces, la solución de esta desigualdad 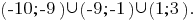 por lo tanto, el menor número entero que es розвязком de esta desigualdad es el número de
por lo tanto, el menor número entero que es розвязком de esta desigualdad es el número de 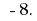
Respuesta: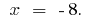


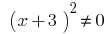 por tanto
por tanto 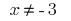 .
.