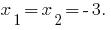二次方程式
定義: 二次方程式  —方程式の形式
—方程式の形式 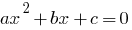 が
が 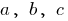 あ番号、
あ番号、 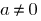
二次方程式の一般形
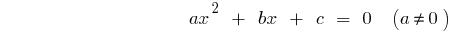
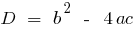 — のdiscriminantsの二次方程式
— のdiscriminantsの二次方程式
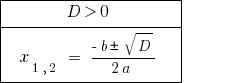
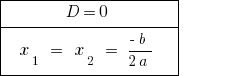
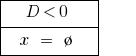
場合 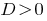 に方程式を二つの異なる。
に方程式を二つの異なる。
場  の方程式は等しい。 時計数のrozwaskiひとつに数えられている値のタイムをお過ごし下さい。
の方程式は等しい。 時計数のrozwaskiひとつに数えられている値のタイムをお過ごし下さい。
時 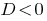 方程式の根があります。
方程式の根があります。
マスター方程式(a=1)
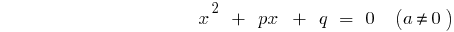
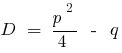 — のdiscriminantsの組合せ式
— のdiscriminantsの組合せ式
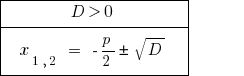
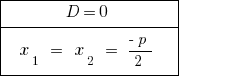
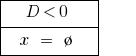
At 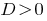 —マスター方程式の二つの異なる。
—マスター方程式の二つの異なる。
き  の方程式は等しい。 時計数のrozwaskiひとつに数えられている値のタイムをお過ごし下さい。
の方程式は等しい。 時計数のrozwaskiひとつに数えられている値のタイムをお過ごし下さい。
場 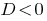 の方程式がない。
の方程式がない。
Vieta定理の一般の場合
場合  の根が二次式
の根が二次式 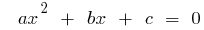 、
、
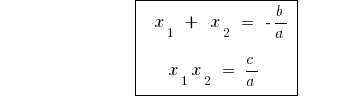
のvieta定理のためのマスター方程式(a=1)
た場合  の連結根の二次式
の連結根の二次式 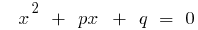 、
、
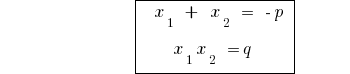
の逆定理の定理のvieta
定理: の場合の和二番号  等
等 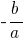 の製品も
の製品も 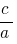 、これらの数字はルーツの二次式
、これらの数字はルーツの二次式 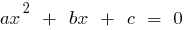 です。
です。
定理(マスター方程式)の 場合の和二番号  等
等 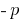 の製品も
の製品も 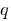 、これらの数字はルーツの二次式
、これらの数字はルーツの二次式 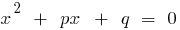 です。
です。
分解エtrinomial要因
場合  の根が二次trinomialゼロに等しい
の根が二次trinomialゼロに等しい 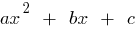 (つまり、ツ方程式
(つまり、ツ方程式 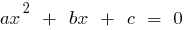 )
)
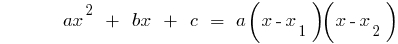
場合にはdiscriminantsスクエアtrinomialはゼロに等しい( )は、
)は、 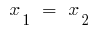 そ
そ
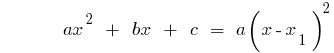
例です。 に分解することにより、trinomialます。
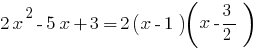
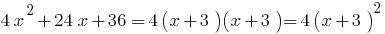
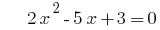 時
時 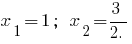
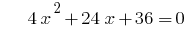 時
時 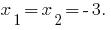

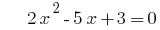 時
時 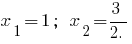
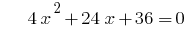 時
時