Возрастающая функция
Определение: Функция  называется возрастающей на некотором множестве
называется возрастающей на некотором множестве 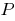 , если большему значению аргумента из этого множества соответствует большее значение функции.
, если большему значению аргумента из этого множества соответствует большее значение функции.
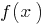 — растет, если для любых
— растет, если для любых 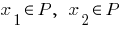
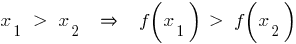
Свойства возрастающей функции
- Если функция
 возрастает на некотором множестве
возрастает на некотором множестве 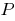 , то большему значению функции соответствует большее значение аргумента из этого множества
, то большему значению функции соответствует большее значение аргумента из этого множества - Сумма нескольких возрастающих на данном множестве функций является возрастающей функцией на этом множестве.
- Если функция
 возрастает, то обратная к ней функция также возрастает.
возрастает, то обратная к ней функция также возрастает. - Если в составленной функции
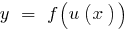 функция
функция 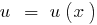 возрастает функция
возрастает функция 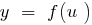 возрастает, то и функция
возрастает, то и функция 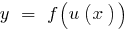 возрастает. Результат последовательного применения двух возрастающих функций - возрастающая функция.
возрастает. Результат последовательного применения двух возрастающих функций - возрастающая функция. - Результат последовательного применения возрастающей и убывающей функции есть функция убывающая.
- Любая растущая на заданном множестве функция каждого приобретает свое значение только в одной точке из этого множества.
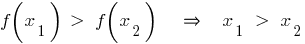
 — возрастающая функция
— возрастающая функция
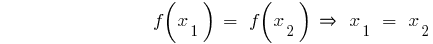 — возрастающая функция
— возрастающая функция
Признак возрастания функции
Если 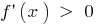 в каждой точке интервала
в каждой точке интервала  , то функция
, то функция  возрастает на этом интервале.
возрастает на этом интервале.
Примеры функций возрастают на всей области определения
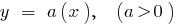
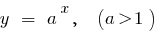
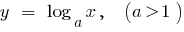
Нисходящая функция
Определение: Функция  называется убывающей на некотором множестве
называется убывающей на некотором множестве 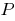 , если большему значению аргумента из этого множества соответствует большее значение функции.
, если большему значению аргумента из этого множества соответствует большее значение функции.
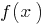 — приходит, если для любых
— приходит, если для любых 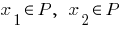
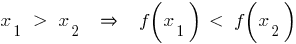
Свойства убывающей функции
- Если функция
 спадаєна некотором множестве
спадаєна некотором множестве 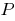 , то большему значению функции соответствует меньшее значение аргумента из этого множества
, то большему значению функции соответствует меньшее значение аргумента из этого множества - Сумма нескольких нисходящих на данном множестве функций является убывающей функцией на этом множестве.
- Если функция
 убывает, то обратная к ней функция также убывает.
убывает, то обратная к ней функция также убывает. - Если в составленной функции
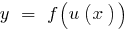 функция
функция 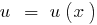 убывает и функция
убывает и функция 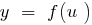 убывает, то функция
убывает, то функция 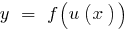 убывает. Результат последовательного применения двух убывающих функций - возрастающая функция.
убывает. Результат последовательного применения двух убывающих функций - возрастающая функция. - Результат последовательного применения возрастающей и убывающей функции есть функция убывающая.
- Любая нисходящая на заданном множестве функция каждого приобретает свое значение только в одной точке из этого множества.
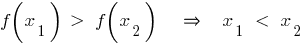
 — убывающая функция
— убывающая функция
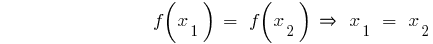 — убывающая функция
— убывающая функция
Признак убывания функции
Если 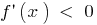 в каждой точке интервала
в каждой точке интервала  , то функция
, то функция  убывает на этом интервале.
убывает на этом интервале.
Примеры функций, спадающими на всей области определения
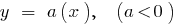
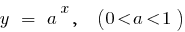
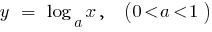

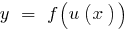 функция
функция 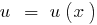 возрастает функция
возрастает функция 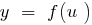 возрастает, то и функция
возрастает, то и функция