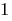Логарифмические неравенства

Определение: Логарифмическое неравенство — неравенство, в котором переменная находится под знаком логарифма.

Чтобы хорошо уметь розвязувати логарифмические неравенства, нужно хорошо уметь владеть опорными соотношениями логарифма.

Равносильные преобразования простейших логарифмических неравенств.

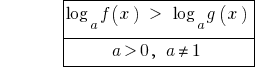
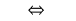
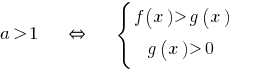
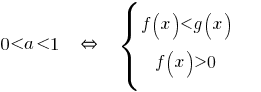
При 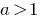знак неравенства не меняется и учитывается ОДЗ.

При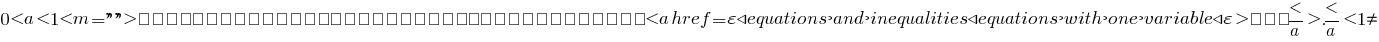

Примеры решению простейших логарифмических уравнений

 

Пример 1

Розвяжіть уравнения: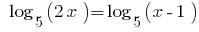

Решения:

Так как 5>1, то функция 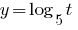— возрастающая и, учитывая ОДЗ, получаем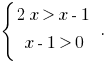

Отсюда 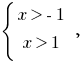то есть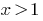

Ответ: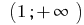

 

Пример 2

Розвяжіть уравнения: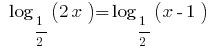

Решения:

Поскольку 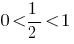, то функция 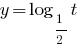— убывающая и, учитывая ОДЗ, получаем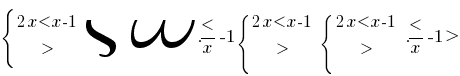

Отсюда 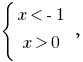— розвязків нет.

Тогда 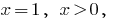то есть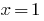

Ответ: розвязків нет.

Схема решению более сложных логарифмических уравнений

1. Использование метода интервалов
2. Использование равносильных преобразований

Как розвязати логарифмическое уравнение

С помощью формул логарифмирования и потенцирования сводим уравнение к простейшему (при этом учитываем ОДЗ начального и следим за тем, чтобы не потерять корни при звужуванні ОДЗ). После преобразований, если не удается свести к простейшего логарифмического уравнения пробуем вводить замену переменных.

Примеры решению логарифмических неравенств

 

Логарифмические неравенства розвязуються так же как и логарифмические уравнения.

Пример 3 (использование формул логарифмирования)

 

Розвяжіть уравнения: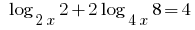

Решения:

Перейдя к основанию 2, получаем равносильные уравнения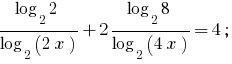

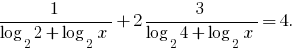
Замена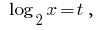

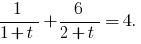
Тогда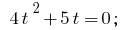

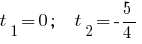
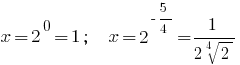
Ответ: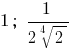

Пример 4 (использование свойств логарифмических функций)

 

Розвяжіть уравнения: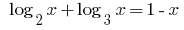

Решения:

Функция 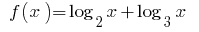возрастает на области определения как сумма двух возрастающих функций, а 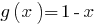приходит. Поэтому заданное уравнение имеет единственный корень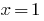

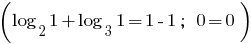
Ответ: